Információ modellek a grafikonok
Home | Számítástechnika és az információs és kommunikációs technológia | Tervezés órák és anyagok órák | 6. osztály | lecke tervezés a tanév (GEF) | Információ modellek a grafikonok
Bemutatása „rendszer”

Információ modellek a grafikonok
Vizuális eszközök bemutatására összetétele és szerkezete a rendszer Earl. Graph áll csomópontok. kapcsolódó vonalak. Ha a vonal irányul (nyíl), akkor az úgynevezett egy ív; vonal irányítatlan (irányítás nélkül) nevezzük egy él. Vonal érkező vertex és egy részét is, az úgynevezett hurok. A csúcsok leírható kör, ovális, pontok, négyszögek, és így tovább. D.
Ha a tárgyak egy olyan rendszer, hogy képviselje a csomópontok és kapcsolatok között - vonalak, megkapjuk az információkat a rendszer típusa, a grafikonon.
Korábban megnéztük a grafikonok - a rendszer kapcsolatok, amelyek tükrözik a meglévő objektumok közötti kapcsolatokat.
Például egy grafikon, amely az arány a „átírt” közötti tárgyak osztálya „gyermek” -ként is szerepelhet ábrán látható. 44.
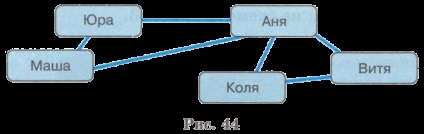
Az arány „felülírja” ( „leveleket írnak egymásnak”) egy kétoldalas (szimmetrikus). Ezért, a megfelelő csúcsok vonalak kötik össze, anélkül, hogy nyilak (élek).
Egy gráf irányítatlan. ha a csúcsait élek kötik össze.
Az útvonal a csúcsok és az élek a grafikon, a grafikon minden szélén, amely nem több, mint egyszer nevezzük egy lánc.
Példa láncok Jura - Anja - Victor - Kohl (lásd a 44. ábrát ..).
Lánc, kezdési és befejezési csúcsok egybeesnek az úgynevezett ciklust.
ciklus példa: Anja - Kohl - Victor - Anya.
Egyébként úgy néz ki, egy grafikon, amely az arány „leveleket” között az azonos osztályú objektumok „gyerekek”. Vonal nyíllal (arc) adja meg egy teljesen más jelentéssel (ábra. 45).
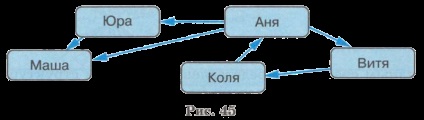
Egy gráf nevezzük orientált. ha a csúcsait köti ívek.
Adjon példákat a lánc és a ciklus a grafikonon látható. 45.
Egy gráf súlyozott, ha a csúcsait vagy élek (ívek) jellemzi néhány további információt - a súlya a csúcsok vagy élei (ívek).
A 46. ábra információt a városok a Golden Ring képviseli egy súlyozott gráf: súlyok a csúcsok - városok, a bázis súlya élek - távolság kilométerben városok között.
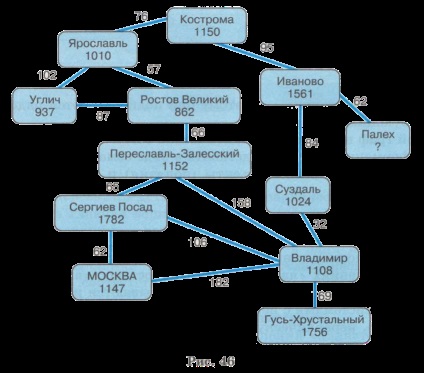
Mik az utak és ciklusok a grafikonon látható. 46.
Graph egy ciklust nevezzük hálózatot.
A 47. ábra képviseli, mint egy grafikon az információs modell egy mese hercegnő Béka.
A gráf - a karakterek és tárgyak a tündérmesékben, az ív - a kapcsolat közöttük. Ellentétben a korábbi példákat,
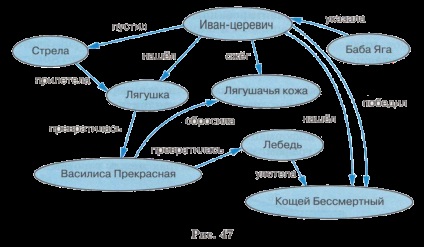
Itt az összes hivatkozást különbözőek. Ezért azok aláírása mellett a megfelelő íveket.
Egy ilyen görbét nevezzük szemantikai hálózat. Úgy véljük, hogy bármilyen információt is képviselteti formájában szemantikai hálózat, amelyben kifogásolja (fogalmak) és linkek (kapcsolatok), megjelenik közöttük.
Hierarchiája - ez elrendezése vagy alkatrészek az egész érdekében a legmagasabbtól a legalacsonyabb. Rendszer, elemei, amelyek a kapcsolat „egyfajta”, „része a” más vonatkozásban és alárendelés nevezett hierarchikus rendszerek (rendszerek hierarchikus struktúra).
Például a hierarchikus szerkezet egy iskola, mert a következőket állapítja meg alárendeltségi viszony: Director - igazgatóhelyettes - tanár - diák.
Systems hierarchikus szerkezettel rendelkező, amelynek az elemeit a összekötve a kapcsolat „egy része.”
A 48. ábrán ábrázolja grafikonon egy hierarchikus rendszer, amely része a szoftver (a szoftver) a számítógépen.
Gróf hierarchikus rendszert nevezzük fa. A megkülönböztető jegye a fa, hogy csak egy út van bármely két csúcsa. A fa nem ciklus vagy hurkok.
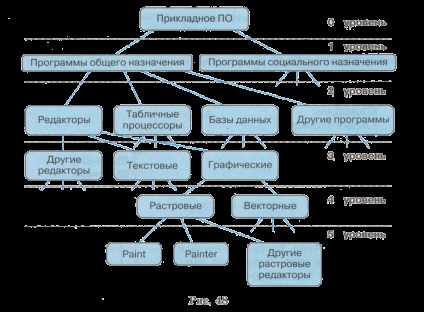
Általában a fa képviselő hierarchikus rendszerben kiosztott egy fő csúcsot, amely az úgynevezett gyökér a fa. Minden csúcsa a fa (kivéve a gyökér) csak az egyik szülő - kijelölő egy objektum belép egy felső szintű osztályban. Bármilyen csomópontja a fa több utódot - megfelelő csúcsokat az alacsonyabb szintű osztályok. Ez a kapcsolat az úgynevezett az „egy a sok”. Felsők, mivel nem keletkezett a csúcsok nevezett levelek.
Treelike rendszerek közötti kapcsolatok „egy faj”, amelyek a láthatóvá besorolása tárgyak (ábra. 49).
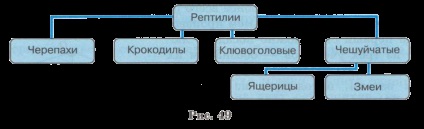
Hierarchia könnyű ábrázolni „létra” - a többszintű lista. Tárgyak az azonos hierarchikus szinten vannak elhelyezve egy szinten a listában. Az alsó szinten a hierarchia, a jobb oldalon van egy lista a megfelelő szinten:
hüllők
teknősök
krokodilok
Klyuvogolovye
pikkelyes
gyíkok
kígyók
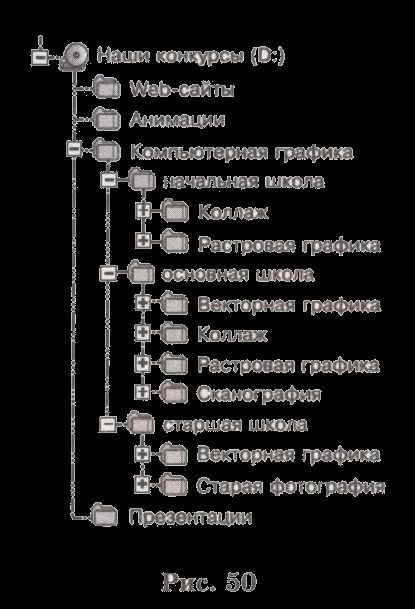
Hierarchikusan szervezett rendszer fájlok tárolására a külső memória. Az operációs rendszer egy fájlrendszer kép a számítógép képernyőjén formájában egy fa (ábra. 50).
A kapcsolat a családtagok kényelmesen képviseli nevű rendszer származástani vagy családfa. Hogy képviselje a családfát lehet bármilyen irányban - ez ízlés dolga modellező.
Gráffal megoldani a problémákat
Grafikonok hasznos megoldásában egyes osztályok problémákat.
Hányféleképpen lehet ülni egy sorban három szék három tanítvány? Írja le az összes lehetséges esetet.
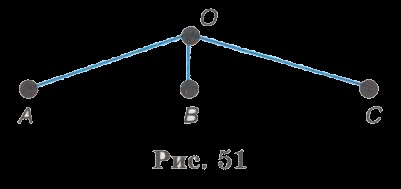
A megoldás erre a problémára a legkényelmesebben képviseli, mint egy fa. Mert a gyökér csomópontot veszünk egy tetszőleges pont O. sík
A szék tudunk bármely a három tanulók - jelölésére az A, B, C reakcióvázlatban L, ez megfelel a három ág egy pontjából kilépő D (51. ábra).
Forgalomba az első tanuló A szék a szék fel a második tanuló B vagy C. Ha az első székre ül a tanuló B, egy második növény lehet A vagy C. Ha az első székre ül C, majd egy második növény lehet A vagy V. Ez megfelel a rendszerben két ága származó minden csúcsa az első szinten (ábra. 52).
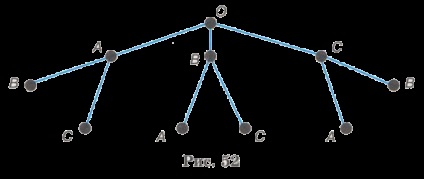
Nyilvánvaló, hogy a harmadik szék, minden esetben úgy a fennmaradó tanuló. Ez megfelel egy ága a fa, amely „nő” az egyes korábbi ágak (ábra. 53).
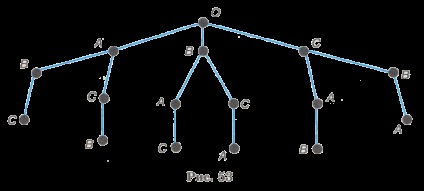
Írjuk le egészen a tetejét az első szinten a harmadik szintre csúcsai: A-B-A-Su C-B, B-A-C, B-C-A, C-A-B, C-B-A. Mindegyik recept módon, hogy meghatározza az egyik lehetőség a diákok ülés a szék. Mivel nincs más út, majd a kívánt számos módon - 6.
A fa nem lehet építeni, ha nem kell, hogy írjon ki az összes lehetőséget, és akkor csak meg kell adnia a számot. Ebben az esetben az ok úgy kell: az első székre ülés lehet az egyik három ember a második - az egyik a másik két, a harmadik - az egyetlen megmaradt: 3-2-1 = 6.
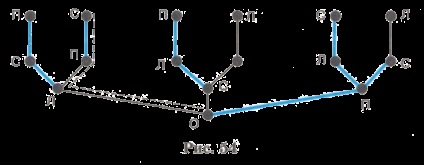
Ahhoz, hogy a cár fiatalító almát, amennyiben Prince Ivan talált az egyetlen biztos módja annak, hogy egy varázslatos kertben. Találkoztam Ivan Tsarevich a vén varjú, és ez milyen tanácsot hallottam tőle három útelágazásnál:
1) megy most a helyes úton;
2) a következő elágazásnál nem választja a helyes utat;
3) a harmadik villa nem megy a bal pálya.
galamb repül már suttogott Prince Ivan, hogy csak egy jótanács varjú hű és biztos, hogy áthaladjon az utak különböző irányokba. Hősünk befejezte a feladatot, és megüt a bűvös kertben. Milyen útvonalon vette?
Jelöljük a bal, középső és jobb utak, illetve az A, C és P. A lehetséges útvonalak vannak ábrázolva egy grafikon. Ugyanakkor tippeket varjú oldalon több „zsír” élek. Mivel csak egy tanácsot távolság megfelelő, akkor a gráf akkor felel meg az útvonalat, amely egy „kövér” él. Ezt az útvonalat jelöli inkább a szaggatott vonal (ábra. 54).
Kérdések és feladatok
1. Adjon példát 2-3 rendszereket, amellyel szembe a mindennapi életben. Információ modellek tárgyak ezek a rendszerek?
2. Minden emeleten az iskolában kell egy menekülési tervet. Keresse meg, és vizsgálja meg. Mely tárgyak jelennek meg a kör?
3. Mely területeken nem nélkülözheti térképek - információs modelleket a Föld felszínén?
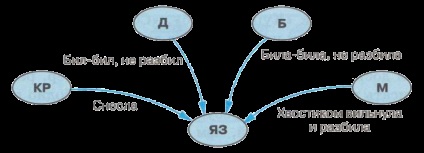
4. Határozza meg a mese, melyek az alábbi grafikon határozza meg a kapcsolat a karaktereket.
5. A különböző oldalain mászni a hegyre, és a három út elvezet a tetején. Sorolja fel a sok útvonalakon, amelyeken lehet mászni a hegyre, és menj le vele. Megoldani ugyanazt a feladatot, ha fel és le menni a különböző utak.
6. Hány háromjegyű szám felírható a számjegyek 1, 3, 5 és 7, azzal a feltétellel, hogy nem kell azonos számjegyek száma a bejegyzéseket?