Hogyan lehet megtalálni a magassága a téglalap alakú piramis
Piramis - poliéder, az alapja, amely egy sokszög, és a másik oldalon - a háromszögek, hogy konvergálnak egy közös csúcs. Problémák megoldására a piramisok típusától függ a piramis. Egy téglalap alakú piramis egyik oldalélén merőlegesek az alapra, ez az él a magassága a piramis.

oktatás
Határozzuk meg az a fajta piramis alapja. Ha az alapja egy háromszög, a háromszög derékszögű piramis. Ha a négyszög - négyszögletes, és így tovább. A klasszikus problémák piramis. melynek alapja egy négyzet vagy egyenlő oldalú / egyenlőszárú / derékszögű háromszög.
Ha az alapja a piramis egy négyzet, megtalálni a magasság (ez - a szélén a piramis) egy derékszögű háromszög. Ne feledje - szilárd geometria a számok négyzet néz ki, mint egy paralelogramma. Például, adott SABCD négyszögletes gúla a vertex S, amely az előrejelzések egy négyzet felső széle B. SB merőleges síkban a bázis. A bordák SA és az SC egyenlő egymással, és merőlegesek az oldalról AD és DC, ill.
Ha a feladat adott, hogy az élek AB és az SA, SB megtalálják a magassága egy négyszögletes SAB a Pitagorasz-tétel. Ehhez vonjuk ki a négyzet négyzet SA AB. Távolítsuk el a gyökér. A magasság a SB talált.
Ha nem adott AB oldalán a tér, hanem például, diagonális, majd emlékezni képlet: d = a · 2. is kifejezetten az oldalán egy négyzet alakú területének a képletek kerületméréseknél beírt és körülírt sugara, amennyiben ez adott abban az állapotban.
Ha a probléma adott a szélén AB és SAB, a tangens: tg SAB = SB / AB. Expressz képletű magasságot. Helyettesítő számértékek, ezáltal megtalálni a SB.
Ha mennyiségének és az alapja a párt, hogy a magas. kifejező ez a képlet: V = · s · h. S - bázis terület, amely AB2- h - a magassága a piramis. t. e. az SB.
Ha az alap a piramis SABC (S vetített B a 2. igénypont szerinti, azaz, az SB - .. magasság) a háromszög, és jelezte adatterület (a oldalon az egyenlő oldalú háromszög, az oldalsó és az alap oldalsó és vagy szögek egy egyenlő szárú, a szárakat téglalap alakú), megtalálja a magassága a mennyiség képletű: V = · s · h. Ehelyett S helyettesítheti egy háromszög területén képlet szerint a fajta, majd kifejezni h.
Ha adott apothem SK verge CSA és az oldalsó AB bázis, keresse meg a SB a derékszögű háromszög SKB. A tér SK kivonni a négyzet KB, SB kap a négyzeten. Távolítsuk el a gyökér és a magas.
Ha adott apothem SK és az a szög között SK és a KB (SKB), egy szinusz függvény. A magasságának aránya a átfogója SB SK egyenlő bűn SKB. Fejezzük ki a magasság, és helyezzük egy számérték.
Bármilyen geometriai test lehet érdekes, nem csak az iskolások számára. A világ körülöttünk meglehetősen gyakori elem a gúla alakja. És ez nem csak a híres egyiptomi sír. Azt szokták mondani, a gyógyító tulajdonságait a piramis, és valaki biztosan szeretné kipróbálni őket magadnak. De ehhez az szükséges, hogy tudjuk a méretek, beleértve a magasságot.

szüksége lesz
- Matematikai képletek és fogalmak:
- Meghatározása a magassága a piramis
- Hasonlóság kritériumok háromszögek
- A tulajdonságok a háromszög magassága
- A tétel a szinusz és koszinusz
- Táblázatai szinusz és koszinusz
- műszerek:
- vonalzó
- ceruza
- szögmérő
oktatás
Emlékszel, mit a magassága a piramis. Ez a merőleges csökkent a tetején a piramis, hogy az alap.
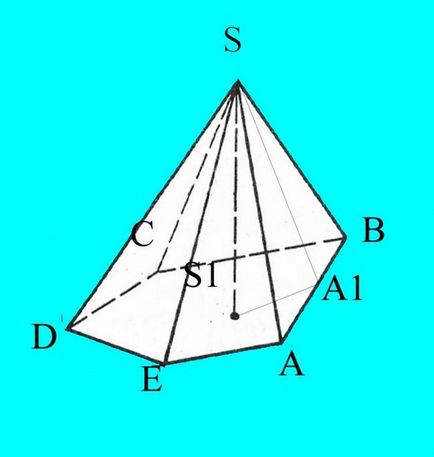
Construct piramis a beállított paraméterek. Kijelöli bázis latin betűkkel A, B, C, D. számától függően a szögek. A csúcs a piramis Mark S.
Tudod az a része, az alapja a sarkok és élek a lejtő aljára. A tervek sikerül vetülete a gépen, így a hűség bélyegét az ismert adatok alapján az Ön számára. Ponttól S alacsonyabb a magassága a piramis és címkézik h. Metszéspontot egy magassága a piramis bázis oboznchte S1.
A piramis csúcsán magasság végezzen oldalán arcát. Jelölje meg a metszéspontot egy bázissal, így például, az A1. Emlékezz tulajdonságait hegyesszögű háromszög magassága. Ez osztja a háromszög két hasonló derékszögű háromszög. Számoljuk ki a koszinuszok derékszögben meg a képlet
Cos (A) = (b2 + c2-a2) / (2 * b * c), ahol a, b, és egy - oldalán a háromszög, ebben az esetben ASB (a = BA, b = AS, c = AB).
Számítsuk ki a magassága az oldalsó felület SA1 ASA1 koszinusza a szög egyenlő a szög SBA tulajdonságok háromszög magassága, és az ismert oldalirányú borda.
Csatlakozás az A1 és S1. Most már derékszögű háromszög, amelyben tudod, átfogója SA1 és az a szög az oldalsó felületek a piramis, hogy az alap SA1S1. Szerint a szinusztétel számítani láb SS1, amely szintén a magasság a piramis.
Kiszámításához a magassága minden piramis szükséges, hogy először kiszámítja az egyik oldalsó háromszög.
A jobb oldallapjának a piramis magasságának nevezzük apothem és oszt félbe a bázis oldalán a piramis.
A jobb oldalon a piramis minden ferde a földre azonos szögben, így a magassága a piramis lehet számítani anélkül, hogy a építési további háromszögek.
A magasság az oldalsó szélén osztja azt két hasonló derékszögű háromszögek. Ennek megfelelően, a SAB szöge egyenlő a szög A1SB.
Figyelem, csak ma!