Hogyan lehet megoldani a problémákat a trapéz
Ahhoz, hogy megértsük, hogyan lehet megoldani a problémákat a trapéz, hasznos emlékezni három alapvető megoldásokat.
I. A magatartás két magasságban.
Ia. Négyszög BCKF - téglalap (hiszen minden szög derékszög). Következésképpen, FK = BC.
AD = AF + FK + KD, így AD = AF + BC + KD.
Háromszögek ABF és dCK - téglalap alakú.
(Belátható egy másik lehetőség:
Ebben az esetben, AD = AF + FD = AF + FK-DK = AF + BC-DK.)
Ic. Ha egy egyenlő szárú trapéz, a megoldás egyszerűsíti a
Ebben az esetben, derékszögű háromszögek ABF és dCK, például, a láb és a átfogója (AB = CD által hipotézis, BF = CK, mint a trapéz magassága). A egyenlőségét háromszögek magában foglalja az egyenlőség az érintett felek:
II. Rajzolj egy párhuzamos egyenes az oldalon.
IIa. BM ∥ CD. Mivel BC ∥ AD (trapéz bázis), majd BCDM - paralelogramma. Ezért MD = BC, BM = CD, AM = AD-BC.
IIb. Különösen egy egyenlő szárú trapéz
BM ∥ CD. Mivel CD = AB, akkor a BM = AB. Vagyis, mi kap egy egyenlő szárú háromszög, és egy paralelogramma ABM BCDM.
III. Továbbra is fél, és kap egy háromszög.
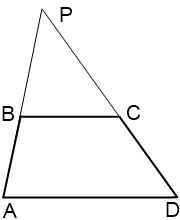
Háromszögek APD és BPC hasonlóak a két sarkában (P szög - összességében, ∠ PAD = ∠ PBC, mint egy megfelelő a BC ∥ AD és metsző AP).
Következésképpen az oldalukra arányos:
Ez a három megközelítés a problémák megoldásához a trapéz - alapanyagok. Ezek mellett számos más módon. Néhány tárgyalt ezen a honlapon. Például itt - hogyan lehet megoldani a problémát a trapéz, amelyek merőlegesek az átlós.