hengeres felületek
Előadás 15. A felületek másodrendű.
Az egyenlet így a háromdimenziós tér határozza meg a felületet. Tehát, már tudjuk a felület egyenlete az elsőrendű - a gépet.
Egy algebrai egyenlet a második és a magasabb rendű a térben határozza felületek, amelyeket az úgynevezett felületei a második és a magasabb rendű. Tekintsük a másodrendű felület egyenlete és egysejtűek.
Forgásfelület egy felület által alkotott forgó térbeli L vonalat (úgynevezett alkotó) egy előre meghatározott körülbelüli L egyenes vonal (úgynevezett forgástengelye) fekvő azonos síkban L (1. ábra).
Nyilvánvaló, hogy a forgás közben a L minden pont kört ír le.
A legegyszerűbb esetben egy felületének forradalom, a L görbe körül forog koordinátatengelyeken.
Által kialakított forgó másodrendű görbék körül szimmetriatengelye, az úgynevezett másodrendű felületek forradalom.
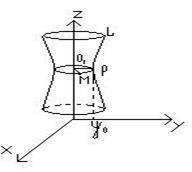
Legyen S - forgásfelület, M (x y z ..) - tetszőleges pontja a felület. Rajzolj egy síkban Oz. ponton áthaladó M. Let O1 metszéspontja a gépet egy Oz. P és pont - egy görbét L. Ezután O1 (0,0, z), és a P (0, y0 z.), Ahol az y0 - néhány számot.
A metszősík a felületi kapott S egy kör; P pont és M feküdni e kör és a kör sugara egyenlő | O1 M | = | O1 P |. Van | O1 P | = | y0 | (Mivel az LÎy Oz), akkor egyrészt O1 M | = | y0 |. Ugyanakkor,
Következésképpen | y0 | =. vagy y0 = ±. Mivel PÎL, akkor a koordinátái kielégítik egyenletek görbét. így F (y0, z) = 0. képviselete itt y0 = ±. megkapjuk
jelenti egy pont koordinátáit M (x y z ..), fekvő rotációs felületen kielégíti az egyenletet F = (±; Z) = 0, akkor ez az egyenlet a következő egyenletet a felületi S.
Hasonlóképpen, az egyik lehet levezetni egy egyenlet felülete körüli forgás további tengelyekre.
Ebből arra lehet következtetni, a következő szabály:
Ahhoz, hogy megtalálja a felület egyenlete L görbe körüli forgás koordinátatengelyeken fekvő azonos síkban L, szükséges egyenlet L görbe változó megfelelő forgástengely, változatlan marad. és egy második változó helyébe (±) négyzetgyöke a négyzetének összege a többi változó.
Például, ha L: F (x y.) = 0, LÎX Oy és forog a tengelye körül Oy. Eq forgásfelület F = (±; z) = 0. Ha a görbe elfordul a tengely körül Ox. A felület egyenlete van írva a formájában F = (x; ±) = 0. Ha L: F (x z.) = 0 körül forgatjuk Oz. akkor a felület egy egyenletet F = (±; z) = 0 stb
Például, ha a kerülete forgatóképesség (y - a) 2 + z 2 = 1 lesz tengelye körül forog, Oy labdát, és amikor elforgatjuk tengely körül OZ - tórusz (Fig.)
Ez a felület az úgynevezett két lapos forgási hiperboloid. Ha úgy deformálja azt, megkapjuk a két ponyvás hiperboloidon
Kitüntetés: 3 négyzet mínusz 2, a megfelelőt.
3) Tekintsük a parabola y 2 = 2pz és elforgatható ezen tengely körül Oz. Kapunk egy felületet az x 2 + y 2 = 2pz. vagy -paraboloid forgatást.
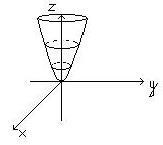
Legyen L - egy bizonyos vonalat az űrben, és l - egyenes, nem feküdt L ugyanabban a síkban.
A hengeres felület van, amely több pontból a térben, amely az unió összes egyenes vonal párhuzamos az adott sorban L, és áthalad a pont a görbén L. A vonal L nevezzük útmutató, és a vonalak párhuzamos vonal L - alakítás hengert.
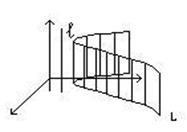
Vegyünk egy hengeres felület alkotói párhuzamosak a tengelyekkel, és a vezetők, hazudik a koordináta síkon.
Legyen L: - térgörbével (nyilván ez síkjában fekszik x Oy), és L = Oz.
Tekintsünk egy hengeres felület. Legyen M (x y, z.) - tetszőleges pontja a felület. Ezután a nyúlvány M1 (x y 0 ..) e pont az x Oy fekszik egy síkban útmutató L. Ennélfogva, a koordinátái x és y kielégíti a egyenletet L:
Ezzel szemben, ha a pont N (x1. Y1. Z1) nem tartozik a hengeres felület, akkor F (x1. Y1) ¹ 0 (N ÏL), azaz egyenlet F (x. Y) = 0, a pontok koordinátáinak felelnek meg a hengerpalást és csak ők, tehát, F (x. Y) = 0 egyenlet a hengeres vezető felület, és egy alkotója párhuzamos az Oz.
Hasonlóképpen ki lehet mutatni, hogy az egyenlet F (x, z) = 0 meghatároz egy hengeres felület egy alkotója párhuzamos Oy és a vezetőtest
Az egyenlet F (y, z) = 0 meghatároz egy hengeres vezető felülete, és egy alkotója, a tengellyel párhuzamos Ox.
A hengeres felület, amelyben a vezetősínnek egy görbe 2. érdekében az úgynevezett hengeres felülete a 2. sorrendben.
Például, a felület (vagy) egy parabolikus henger.
Felületi egyenlet vagy - ellipszis henger:
Egyenletek és meghatározzák a hiperbolikus henger: