funkciós vizsgálatban a maximumok és minimumok a származékos
Hogy végezzen vizsgálatot az adott funkció a minimum és maximum két módja van:
- szerinti első deriváltjának - $ f „(x) $;
- egy második származék - $ f '' (x) $.
kutatási algoritmus felhasználásával az első derivált a következő lépéseket tartalmazza:
- megtalálása az első származékot egy adott funkció - $ f „(x) $;
- megtalálása kritikus pontok ($ f „(x) = 0 $, vagy nem létezik);
- tanulmány jel $ f „(x) $ keresztül a számegyenesen;
- természetének meghatározása a kritikus pont;
- értékének kiszámításakor $ f (x) $ minden egyes kritikus változó értékét.
Minden lehetséges opciókat, ami történhet eredményeként a tanulmány foglalja össze egy táblázatban.
Fedezze fel a megadott függvény a legkisebb és a legnagyobb: $ y = 3x ^ -5x $.
Találjuk az első származékot egy adott funkció: $ y '= (3x ^ -5x)' = 6x- 5 $.
A kritikus pontok:
Mivel a származék egy adott funkció megváltoztatja jelet „-” és „+”, akkor van egy minimális pontot.
Számítsuk ki a értéke egy előre meghatározott függvény legalább:
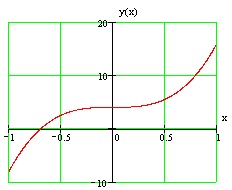
A grafikon egy adott funkció ábrán látható.
Találjuk az első származékot egy adott funkció: $ y '= (3x ^ 2)' = 9x ^ $.
A kritikus pontok:
- Mivel a származék az adott funkció nem változik jel, amikor áthalad a kritikus pontot, ezen a ponton nincs korhatár.
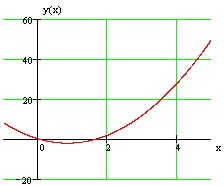
A grafikon egy adott funkció ábrán látható.
A tanulmány az adott funkciót a minimális és maximális a második származékot kell használni a következő tétel.
Tekintsük az $ y = f (x) $. Legyen $ $ x_ - a kritikus pont ($ f „(x_) = 0 $).
Ezután, ezt a funkció maximum egy kritikus ponton $ x = $ x_, ha $ f '' (x_) 0 $.
Ha a $ f „” (x_) = 0 a kritikus ponton $ $ x = $ x_, akkor ez a funkció $ y = f (x) $ nem határozható meg a második deriváltja a természet a kritikus pont.
kutatási algoritmus felhasználásával az első derivált a következő lépéseket tartalmazza:
- megtalálása az első származékot egy adott funkció - $ f „(x) $;
- megtalálása kritikus pontok ($ f „(x) = 0 $, vagy nem létezik);
- meghatározása a második származékot az adott funkció - $ f „” (x) $;
- tanulmány jel $ f „” (x) $ a kritikus pont,
- természetének meghatározása a kritikus pont;
- értékének kiszámításakor $ f (x) $ minden egyes kritikus változó értékét.
Minden lehetséges opciókat, ami történhet eredményeként a tanulmány foglalja össze egy táblázatban.
Fedezze az adott funkciót a minimális és maximális: $ y = 12x ^ + $ 4.
Találjuk az első származékot egy adott funkció: $ y '= (12x ^ 4)' = 36x ^ $.
A kritikus pontok:
Mi található a második deriváltja az adott funkció: $ y '= (36x ^) „= 72x $.
Vizsgáljuk meg a jel $ f '' (x) $ a kritikus pont: $ y '(0) = 72 \ cdot 0 = 0 $
Mivel a második származékot adott funkció eltűnik a kritikus pont, nem tudjuk meghatározni a természet egy kritikus pontot vele.
Annak meghatározására, a természet a kritikus felhasználás helyén az első derivált. Megvizsgáljuk a jele $ f „(x) $ segítségével a szám sor:
- Mivel a származék az adott funkció nem változik jel, amikor áthalad a kritikus pontot, ezen a ponton nincs maximum vagy minimum
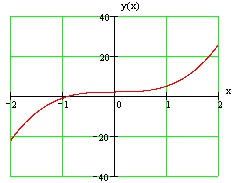
A grafikon egy adott funkció ábrán látható.