Field egyenletesen töltött sík
Tegyük fel, hogy egy végtelen síkot (Fig.3.5) van egyenletesen töltött egy felületi töltéssűrűség ( = dQ / DS a töltés egységnyi felület).
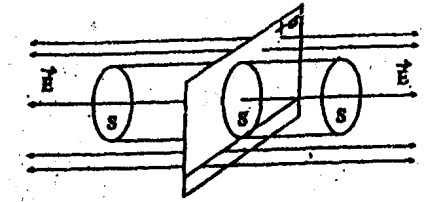
Isolate egy síkban területen S és körülveszik a hengeres zárt felület egy bázissal, párhuzamos síkban. Mivel a vonal E vektor merőleges a sík és párhuzamos, a generátorok a henger, a teljes áramlás egy zárt, hengeres felület összegével egyenlő áramlások csak a két alapjának:
Szerint a tétel a Gauss-Ostrogradskii
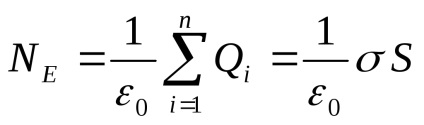
Egyenlővé a jobb oldalán, N, megkapjuk
Tól (3.11), ebből következik, hogy a térerősség a végtelen sík felszámított pont nem függ a távolság nekik. Következésképpen, a mező homogén sík.
Field két ellentétes töltésű végtelen párhuzamos síkokban (3.6 ábra)
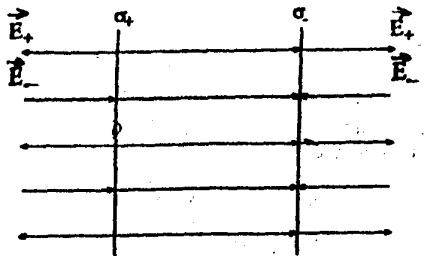
Tegyük fel, hogy a felületi töltés sűrűség síkok + i -ravny legnagyobb. Amint az a 3.6 ábra, erővonalak a bal és jobb oldalán a síkok egymás felé. Ezért, a teljes térerősség E = 0 síkok. A területen a síkok közötti, tekintettel (3.11).
Így a mező homogén síkok közötti. És lehet tekinteni, mint homogén erőtér belsejében a véges párhuzamos síkokban (planáris kondenzátor).
Dolgozz elektrosztatikus mező erők mozgatásakor díjat. potenciális
Oh
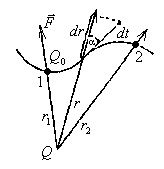
Mivel a díj mozgó Q0 erejét kölcsönhatás zaryadomQ. Létrehoz egy mezőt a Coulomb-törvény függ rasstoyaniyar:
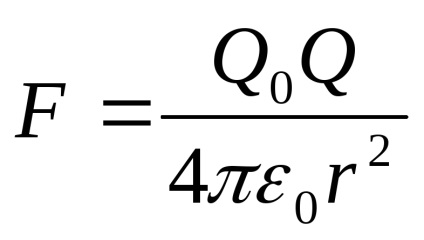
előbb meg kell adni az elemi munka Dana végtelenül uchastkedℓ:
Itt α - közötti szög vektorok Fidℓ. Mivel chtodℓcosα = dr találunk a teljesítményét az integrál:
Ebből következik, hogy a művelet az elektromos mező nem függ az alak a útvonal, által meghatározott kezdeti és a végső pozíciók Q0 töltés. Ez azt jelenti, chtoelektrostaticheskoe mező potenciálja, teljesítmény - konzervatív.
(3,13) azt mutatja, hogy a végzett munka a mozgó töltés elektrosztatikus térben mentén bármely zárt kontúr egyenlő nullával, azaz:
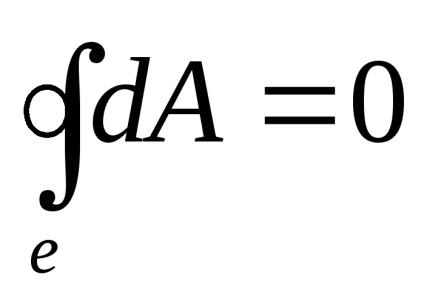
Az utolsó egyenlőség felírható, tekintettel arra, hogy
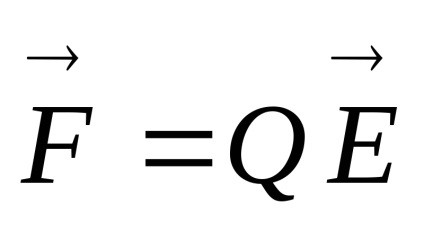
Ezután az elektrosztatikus tér, van:
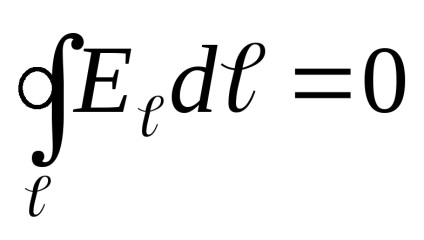
ahol Eℓ = E sosα- vetülete a vektor E peremescheniedℓ.
Ez az integrált hívják a forgalomban az elektrosztatikus tér vektor napryazhennosti.Dlya forgalomba mentén bármely zárt nulla.
A „mechanika” tudjuk, hogy a munka a konzervatív erők egyenlő a veszteség potenciális energia:
Összehasonlítva a fenti egyenlet (3.13), megkapjuk képlet Q0 töltés potenciális energiája. található a zaryadaQ:
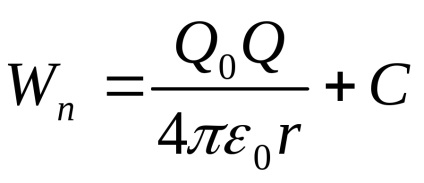
Mivel a távolság a Q töltésű, és a potenciális energia csökken lehet kiindulni, hogy a beskonechnostiWp = 0, az integrációs konstans
Az arány Wt / Q0 független a töltés, és sluzhitenergeticheskoy jellemző területén. nazyvaemoypotentsialom mező egy adott ponton létrehozott zaryadomQ:
Képletek (3,14) és (3.15), hogy a potenciális egy ponttöltés mező (ballon) Q:
Által végzett munka elektromos erők mozgó töltés Q0 ponttól 1 és 2 pont, ki lehet számítani keresztül a potenciálkülönbség:
Ha a 2. pont található a végtelenben, φ2 = 0, és ezért
ahol Q0 a nagysága a töltés szállítják a területen.
Így lehetséges az pont a mező határozza meg a munkát a területen erők mozgatása közben egy egységnyi töltést, hogy pont a végtelenig. Az egység potenciális prinyatVolt:
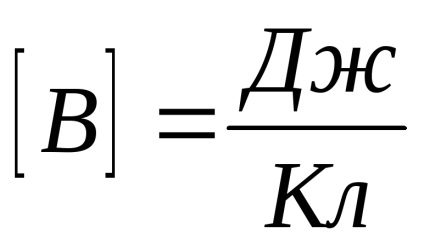
a kapacitás a jel előjele határozza meg a díj, ami egy területen. Ha a mező van kialakítva egy adózási rendszert, annak lehetséges egyenlő az algebrai összege potenciális területeinek valamennyi költséget (szuperpozíció elve)
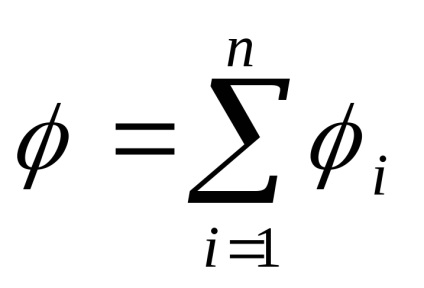
A pontot a térben egyenlő potenciálok felületet képez nevű ekvipotenciális. Egy ilyen felület, például, egyenletesen feltöltött felülete a vezetőképes gömb.
Működés a töltés Q váltakozó mentén ekvipotenciális poverhnostiA = Q Δφ = 0.