Elektrosztatika példák problémamegoldás
elektrosztatika
Példák problémák megoldása
W
Összefüggés adja meg: m1 = m2 = m = kg - tömege golyó, a távolság a golyó, - a szögben, amelyet a fonalak, a dielektromos állandó, Kd - a töltés az elektron.
Keresés: Q- kezdeti töltése a labdát; N - felesleges elektronok számát minden egyes izzó.
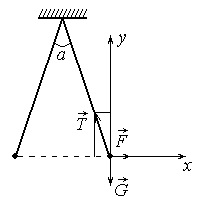
Határozat. Mivel a probléma nem szerepel közepes feltételezik, hogy a díjak kölcsönhatásba vákuumban. A törvény szerint a megőrzése töltés érintkező golyók minden ezek fogja terhelni q / 2. A golyók három erő: a gravitációs erő G = mg. szálfeszítő erő T reakció, az erőt a villamos interakció
Abban az esetben, egyensúlyát algebrai összege előrejelzések ezen erők a függőleges és vízszintes irányban egyenlő nullával:
T · cos (α / 2) - mg = 0, F - T · sin (α / 2) = 0
Megoldása egyenletrendszert F. kapni:
Behelyettesítve F értéket a képlet a Coulomb-törvény, megkapjuk azt a kifejezést q töltéssel.
Tekintettel arra, hogy minden labdát volt töltve, meghatározzák n =.
Behelyettesítve számszerű adatok, megkapjuk
Mi található a felesleges elektronok számát az egyes izzó:
: A bevezető labda díj megegyezik 7,3 · 10 Cl; a felesleges elektronok számát minden egyes izzó mintegy 4,6 · 10.
Feladat. Lemezkondenzátor, a terület minden egyes lemez 6,2 × 10 -3 m 2 csillámmal töltött relatív dielektromos állandója 6. A lemezek közötti távolság 2,00 mm. Határozza meg a villamos kondenzátor kapacitása, a potenciálkülönbség a lemezek, a mező intenzitása egy kondenzátor és a kölcsönös vonzóerő a lemezeket, ha a töltést mindegyik egyenlő 4,00 × 10 -8 Kd.
Ez adja meg: S = 6,2 · 10 -3 m 2 - egy lemez terület, d = 2,00 · 10 -3 m - a lemezek közötti távolság, ε ε = 6 - relatív dielektromos állandója a közeg, q = 4,00 · 10 Cl -8 - töltés egy lemez, ε0 = 8,85 · 10 -12 F / m - az elektromos állandó.
Keresés: C - elektromos kondenzátor kapacitása; U - a potenciális különbség a lemezeken; E - mező intenzitása egy kondenzátort; F - az erő a kölcsönös vonzás lemezek.
Határozat. Villamos kapacitás a kondenzátor által meghatározott általános képletű kapacitás lapos kondenzátor:
Ismerve a töltés q és a C kapacitás meghatározni a potenciális különbség a kondenzátor lemezei:
A térerősség belsejében a kondenzátor és a potenciális különbség keresztben lemezek összekötött kapcsolatban
Mivel a mezőbe a két lemez kapjuk szuperpozíciójával a két terület (Mindkét lemez) egy lemez térerősség E „= E / 2. Az az erő, amellyel az egyes lemezek vonzza egy másik,
Numerikus adatokat a rögzített feltételeket a problémát, és a képlet, mi határozza meg az ismeretlen mennyiségek:
Válasz. Elektromos kapacitású kondenzátor 1,65 · 10 -10 F; potenciális különbség a lemezeken 242; térerősség kondenzátorok 1,21 · 10 5 V / m; az erő a kölcsönös vonzás lemezek 2,42 ·· 10 -3 N.
Feladat. Határozza meg a villamos kondenzátor kapacitása, amely gyártásához használt alumínium fólia szalag hossza 157 cm, szélessége 90,0 mm. Viaszos papír vastagságának 0,10 mm. Mi az energia tárolása a kondenzátor, ha fel van töltve az üzemi feszültség 4,0 × 10 2?
Összefüggés adja meg: L = 157 cm = 1,57 m - hossza alumínium fólia, H = 90,0 mm = 9,0 x 10 ~ 2 M - fólia szélessége, d = 0,10 mm = 0,10 × 10 -3 m - vastagsága viaszos papír, U = 4,0 · február 10 B - feszültség a kondenzátor lemezeket, - a dielektromos állandó, ε = 2,0 - relatív dielektromos viaszpapírral.
Keresés: C - elektromos kondenzátor kapacitása, W - energia kondenzátor.
Határozat. Ahhoz, hogy megtalálja az elektromos kapacitás képlet segítségével
kondenzátor energia képlettel számítottuk ki
A numerikus adatok a feltételeket, a probléma, azt látjuk,
Válasz. Villamos kapacitás a kondenzátor 25 microfarad · 10 -3; az energia a kondenzátor 2 mJ.
Feladat. Három kondenzátor kapacitása C1 = 0,2 uF C2 = C3 = 0,4 uF csatlakoztatva séma szerint az ábrán látható, és csatlakozik egy egyenfeszültség-forrásra UAV = 250 B. Keresse a teljes töltés, a díjak és a potenciálkülönbség az egyes kondenzátorok. Határozzuk meg a tárolt elektromos energia akkumulátor kondenzátorok.
Adott: C1 = 0,2 × 10 -6 F, C 2 = C 3 = 0,4 × 10 -6 F - elektromos kapacitású kondenzátorok UAV = 250 - feszültség a kondenzátort.
Keresés: q, Q1, Q2, Q3 - a teljes díj és a kondenzátor töltésének; U1, U2, U3 - potenciális különbség az egész lemez kondenzátorok, W - tárolt villamos energia minden kondenzátorok.
Határozat. Ismeretlen általános töltés van meghatározva képletű
ahol a C - elektromos kondenzátor kapacitása (akkumulátor) - összekeverjük a képlet (párhuzamos és soros) csatlakozások:
A díj az első kondenzátor megegyezik a teljes hiteldíj:
és díjakat a másik két kondenzátor
q2 = q3 = q / 2.
Ismerve a kapacitás és a felelős minden kondenzátor, meg tudjuk találni a potenciális különbség azok lemezeken.
Ahhoz, hogy megtalálja a tárolt energiát egy elem kondenzátorok, használja a képlet
Mi található a tárolt töltés akkumulátor:
A díjakat az egyes kondenzátorok:
Kiszámítjuk a potenciális különbség és a teljes energia:
Válasz. Az akkumulátor töltöttségi szintjét, és az első kondenzátor, a második kondenzátor és a harmadik - a; potenciál különbség: 200.50 és 50B; az összes energia.