Egységgyök
Ezekből képletek az következik, hogy az egységgyök mindig pontosan n. és ezek mind különböző.
geometriai tulajdonságok
- Minden gyökér modul 1. A komplex síkon az egységgyök alkotják a csúcsai szabályos sokszög. írva a készülék körben. Az egyik csúcsot mindig integrált egység 1 + i 0.
- Ha u k> - a gyökér az egység, akkor a konjugált rá az u k ¯ >>> - szintén gyökere egységét.
- Legyen M - tetszőleges pont az egység kör, és n> 1. Ekkor a négyzetének összege a távolságok M minden n-edik egységgyök egyenlő 2 N.
algebrai tulajdonságai
- Az egységgyök van algebrai egészek.
- A egységgyök által alkotott szorzás kommutatív véges csoport n-edrendű. Különösen olyan szerves erő gyökerét egység is gyöke egységét. Fordított az elem minden egyes eleme a csoport egybeesik a konjugátum. Semleges eleme a csoport a komplex egységet.
- gyökerei egységek csoportja izomorf az adalékanyag csoport maradék osztályok Z n _>. Ebből következik, hogy ciklikus; például egy magot (primitív) vehet minden u k> elemet. A k index relatív prím a n.
- következmények:
- Az elem u 1> mindig primitív;
- ha n - elsődleges. mértékig bármely gyökere, mint ± 1. Ez magában foglalja az egész csoport;
- száma primitív gyökerek egyenlő φ (n). ahol φ - Euler funkciót.
- következmények:
- Ha n> 1. akkor az összeg a fokozatok primitív egységgyök u volna a képlet:
- Π k = 1 n - 1 | 1 - u k | = N (n> 1) ^ | 1-u_ | = n \ qquad (n> 1)>

Cube egységgyök
Cube egységgyök:
A gyökerek a 4. fokú egységet:
A gyökér 5. fokú generáló elem 4:
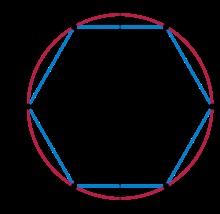
Roots 6. egység, mint az első fokú a generáló elem