Differenciálegyenletek - Általános információk és alkalmazási
Tanulás a természeti jelenségek, megoldására különböző feladatokat a közgazdaságtan, biológia, fizika, technika, nem mindig lehetséges azonnal közvetlen kapcsolatot között az egyes értékek, amelyek leírják egy adott fejlődési folyamat. Általában meg lehet határozni a kapcsolatát ezeket az értékeket (funkció) és a változás mértéke tekintetében a többi (független) változó. Ez felveti
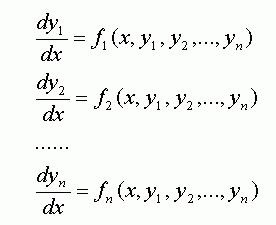
Differenciálegyenletek:
1) Hagyományos egyenletet I-edrendű, integrálva vannak a négyzetek. Ezek viszont, vannak osztva: differenciálegyenletek elkülöníthető változók; Vezérlés elválasztjuk változók; egységes ellenőrzési; lineáris kontroll; Pontos differenciálegyenletek.
2) ellenőrzését magasabb rendű.
3) Lineáris Control II-edrendű, amelyek homogén lineáris II kontroll-edrendű állandó együtthatós, inhomogén lineáris vezérlő állandó együtthatós.
Ellenőrzés akkor is megoldható több módon, a leggyakoribb, amely - a Cauchy probléma, a módszerek Euler és Bernoulli, és mások.
Sok problémát a közgazdaságtan, matematika, technika kell számítani bizonyos számú kapcsolatos funkciók egymást egy bizonyos mennyiségű ellenőrzés. Aztán jön a támogatás a rendszer differenciálegyenletek: egy sor egyenletek, amelyek mindegyike tartalmaz egy független változó, a funkciója ennek a független és ezek származékai.
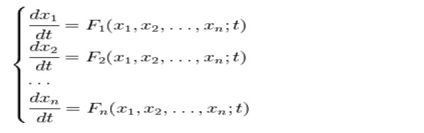
Ha a rendszer lineáris az ismeretlen függvények, ez az úgynevezett lineáris differenciálegyenlet-rendszert. Normál differenciálegyenlet-rendszert lehet helyettesíthetők egyetlen vezérlő, a sorrendje, amely egyenlő a számát egyenletek.
Conversion vezérlőrendszer egy egyenletet néhány esetben hajtjuk végre, hogy az eliminációs módszer.
Amellett, hogy az összes fenti, ahány lineáris rendszerek állandó együtthatós, amely könnyen megoldható Euler módszerrel.

