Deformáció a feszültség és a tömörítés
Deformáció a feszültség és a tömörítés
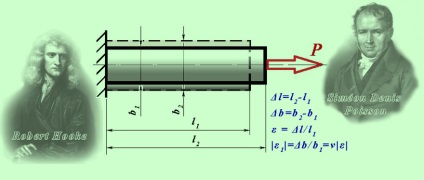
Hosszirányú húzási és nyomási
A természet a törzs, amely ki van téve a közvetlen gerendát húzó vagy nyomó, meghatároztuk, amelynek tapasztalattal rendelkezik a gumi elemet, amelyen a vonal rács került alkalmazásra.
Most képzeljük el, a sugár állandó hosszúságú szekciója l. amelynek egyik vége be van fogva, és csatlakozik a szabad végén a húzóerő F. Ez az erő bar hosszabbítva mennyiségben DL. amely nevezünk abszolút kiterjesztése gerenda.
Az arány az abszolút nyúlása AL, hogy az eredeti hossza a rúd L hívják nyúlást, és hagyja, ε:
ε = AL / l
Nyúlás - dimenzió és néha százalékban kifejezve.
Tehát, gerenda alakváltozás a feszültség és a tömörítés jellemzi abszolút és relatív hosszának változtatása, vagy zsiradék.
Hooke-törvény húzásra és nyomásra
Stressz és a feszültség és a tömörítés összekapcsolt lineáris, amely az úgynevezett törvénye Hooke. miután az angol fizikus Robert Hooke (1653-1703 év), aki létrehozta a törvény.
Fogalmazza Hooke-törvény is olyan: a normál feszültség egyenesen arányos a nyúlás vagy zsiradék.
Matematikailag ez a kapcsolat van írva a következő:
σ = E ε.
Itt E - arányosság tényező, amely jellemzi az anyag merevsége a fa, így képes ellenállni deformáció .. ez az úgynevezett Young-modulus. vagy rugalmassági modulusa az első fajta.
Modulusz, mivel a feszültség kifejezett pascalban (Pa).
Az értékek E különböző anyagok vannak beállítva kísérletileg, empirikusan, és annak értéke megtalálható a megfelelő könyvtárakat.
Így, az acél E = (1,96. ... 2,16) x 105 MPa réz E = (1,00. 1,30) × 105 MPa, és t. D.
Meg kell említeni, hogy a Hooke-törvény csak akkor érvényes, egy bizonyos tartományon belül a rakodás.
Ha a képlet a Hooke-törvény, hogy helyettesítse a korábban kapott értékek nyúlás és a stressz: ε = AL / l. σ = N / A lehetséges kapjuk az alábbi összefüggést:
AL = N l / (E A).
A terméket a rugalmassági modulus a keresztmetszeti területe A × E. a nevezőben, úgynevezett keresztmetszeti merevség feszültség és a tömörítés; ez jellemzi mind a fizikai és mechanikai tulajdonságait a fa anyag és a geometriai méretek a keresztmetszet a fa.
A fenti képlet Hooke-törvény csak akkor érvényes, bárok és szakaszok, amelyek keresztmetszete állandó készült ugyanabból az anyagból, és állandó erővel. A fűrészáru, amelynek több szakasza különböző anyagi, keresztmetszeti méretei a hosszirányú erő, a változás hossza az összes fát úgy definiáljuk, mint az algebrai összege meghosszabbítása vagy lerövidítése az egyes szakaszok:
AL = σ (δli)
Alatti keresztirányú alakváltozás feszültség és a tömörítés
Korábban leírt tapasztalatok gumi gerenda, amelyen rácsvonalak alkalmazott, azt mutatta, hogy a nyúlási keresztirányú méretei a gerenda csökken, és a tömörítés - növekszik, azaz, a sugárnyaláb válik akár vékonyabb vagy vastagabb ... Ez a jelenség jellemző a táblák készült összes anyag.
Tapasztalati úton találtuk, hogy az egytengelyű húzó vagy nyomó aránya a relatív keresztirányú és hosszanti törzs egy adott anyag - állandó.
Ez az első alkalom ez a kapcsolat egy francia tudós, S. Poisson (1781-1840 év), és ez matematikailag írható:
ahol ν - keresztirányú deformációs együttható, az úgynevezett Poisson.
Poisson-tényezője pedig egy dimenzió nélküli mennyiség, és jellemzi az elasztikus anyag tulajdonságaira. A feszültség és a tömörítés, ez a koefficiens venni egyenlő.
Az értékek Poisson különböző anyagok vannak beállítva empirikusan és értékek megtalálhatók az adott könyvtárakban.
Potenciális energia húzóierheiésse
A statikus (alacsony) húzó mintának F húzóerő nullától bizonyos értéket, meghosszabbítja a minta érték DL és így végez munkát W.
Ez a munka felhalmozódik a deformált mintában formájában deformációs energia U. és elhanyagolja kisebb energiaveszteséget (például termikus), feltételezhetjük, hogy W = U.
Tanulmányozva a diagramok nyújtás a minták, azt találtuk, hogy a potenciális energia a rugalmas deformáció a rúd hossza l A állandó keresztmetszetű azonos minden szakaszának a hosszirányú erő N = F lesz egyenlő:
U = W = F AL / 2 = N 2 l / (2E A)
Ellenállás anyaga is működik egy olyan kifejezés, mint a konkrét helyzeti energiája deformáció. amelynek kiszámítása a potenciális energia egységnyi térfogatú fa.
A egyidejű hatása húzó és nyomó terhelések vagy lépésenként változó keresztmetszeti gerenda mérete, van osztva egységes szakaszok és az egyes számít a potenciális energia a deformáció. A potenciális energia deformációja az egész faanyag kerül meghatározásra összege potenciális energia az egyes szakaszok.
Elemezve a potenciális energia deformációs képlet, arra lehet következtetni, hogy ez a mennyiség mindig pozitív, mert a kifejezés magában foglalja a négyzetek lineáris és teljesítmény mennyiségben. Emiatt a számítás a potenciális energia deformáció nem lehet alkalmazni a szuperpozíció elve (mert a tér az összeg nem egyenlő a négyzetének összege a feltételeket).
Az egység deformációs energia munka joule (J).
Anyagok a „feszültség és a tömörítés”:
- Fogalmak húzó alakváltozás és a tömörítés.
- Számítások a szakítószilárdság és a tömörítés. Statikailag határozatlan probléma.