Csökkentési képlet szabályok és menetrendek példák
Ahhoz, hogy használni csökkentési képlet, két szabályt.
1. Ha a szög is képviselteti magát (π / 2 ± a) vagy (3 * π / 2 ± a), a függvény neve megváltozik a bűnnek cos cos bűnre, tg a ctg, CTG a tg. Ha a szög jelölhető (π ± a) vagy (2 * π ± a), a függvény nevét változatlan marad.
Nézd meg az alábbi képre, sematikusan ábrázolt mikor kell változtatni a jel, és mikor nem.
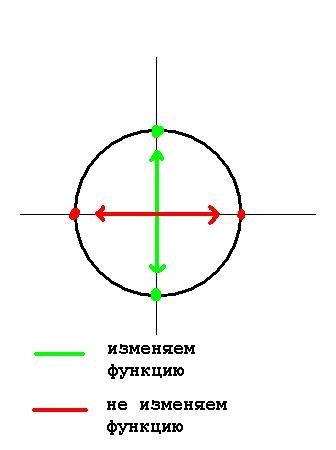
2. A szabály „mint te, így maradtam.”
A jel fenti függvény ugyanaz marad. Ha az eredeti funkciója volt „plusz” jel, akkor a fenti funkció „plusz” jel. Ha az eredeti funkciója volt a „mínusz” jel, akkor a fenti függvény a jele „mínusz”.
Az alábbi ábra mutatja a főbb jelei trigonometrikus függvények, attól függően, hogy a negyedév során.
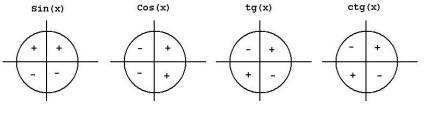
Mi használja a fenti képlet:
Sin (150˚) van a második negyedévben, ábra látható, hogy a jele bűn ebben a negyedévben is +. Tehát a fenti függvény is „plusz” jel. Ez azt használta a második szabályt.
Most 150˚ = 90˚ + 60˚. 90˚ van tc / 2. Ez foglalkozik esetén π / 2 + 60, így az első szabály változás funkció sin és a cos. Ennek eredményeképpen megkapjuk Sin (150˚) = cos (60˚) = ½.
Ha szükséges, amely az összes, a képletek lehet csökkenteni egy asztalon. De könnyebb megjegyezni a két szabályt, és használja őket.