Bernoulli differenciálegyenlet, példák, oldatok
Ebben a cikkben fogjuk megvitatni megoldási módjait, Bernoulli-egyenlet. Megszilárdítása az anyagot részletesen vizsgálni a megoldás a példák.
Bernoulli differenciálegyenlet formájában van. Ha n = 1, ez az egyenlet válik differenciálegyenlet elkülöníthető változók.
Az egyik megoldási módjait, a Bernoulli-differenciálegyenlet, hogy csökkentsék azt a lineáris inhomogén differenciálegyenlet az első, hogy a bevezetése egy új változó. Sőt, van egy differenciálegyenlet és Bernoulli megnézzük az ilyen helyettesítés
Mivel a differenciálegyenlet csökkenti a Bernoulli lineáris inhomogén differenciálegyenlet az elsőrendű. Megoldása után ez az egyenlet, és az inverze a helyettesítési megkapjuk a kívánt megoldás.
Nézzük a következő példát.
Keresse az általános megoldás a Bernoulli-egyenlet.
A példánkban. Bemutatjuk az új változó, akkor. Miután a változás a változó és kis átalakítások megkapjuk az elsőrendű LNDU
Mi megoldjuk a módszer variációs tetszőleges állandók.
Ehhez először azt látjuk, az általános megoldás a differenciálegyenlet.

Z = 0 is megoldás egy differenciálegyenlet, mivel válik identitás függvény nulla z. Ez az eset lehet leírni az egyenlet, ha c = 0. Tehát, az általános megoldás a differenciálegyenlet, ahol C - tetszőleges konstans.
Most változik a tetszőleges konstans, azaz, fogadja az általános megoldás a differenciálegyenlet. ezért
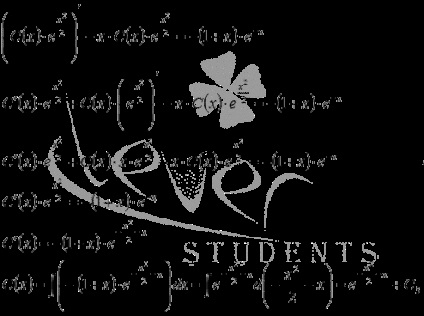
ahol C3 - tetszőleges konstans.
Így.
Ez maradt tölteni az inverz változás. Mivel feltettük, hogy. Ez egy általános megoldás az eredeti Bernoulli-egyenlet.
Tekintsünk egy másik megoldási módja az Bernoulli differenciálegyenlet alapján a képviselet a funkciója ismeretlen y, mint a termék funkciók u (x) és v (x).
Ebben az esetben. Behelyettesítése után a Bernoulli-egyenlet megkapjuk
Ha a függvény v nulla hogy egy partikuláris megoldása a differenciálegyenlet érkezünk egyenlőségét
hol és funkciójának meghatározása u.
Mi megoldjuk a példa ilyen módon világossá vált, hogy az összes.
Problémák Cauchy probléma, y (0) = 1.
Más szóval, meg akarjuk találni egy adott megoldást a differenciálegyenlet kezdeti állapot y (0) = 1.
Miután elosztjuk mindkét oldalon 2 x + 1 egyértelmű, hogy van eltérés Bernoulli-egyenlet.
Először is, azt látjuk, az általános megoldás.
Tegyük fel, hogy y = u ⋅ v. akkor az egyenlet
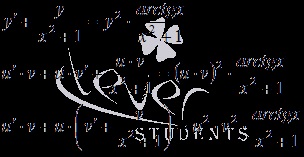
Találunk egy partikuláris megoldása a differenciálegyenlet elkülöníthető változók, nullától eltérő.
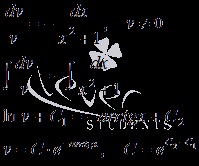
Vegyük saját megoldásokat.
Mielőtt veszi az egyes integrálok külön megjegyezzük, hogy u = 0 megoldás.
Az integrál a bal oldali, könnyen megtalálható a táblázatból primitívek:
Ahhoz, hogy megtalálja az integrál arctgx = z elfogadja és használja a módszert integrálás:

Honnét - minden döntést a Bernoulli-egyenlet.
Továbbra is találni egy adott megoldást kielégíti a kezdeti feltétel y (0) = 1. óta, akkor. Következésképpen ,.
Így, - a kívánt oldatot a Cauchy probléma.
- Èl'sgol'ts LE Differenciálegyenletek és variációszámítás.