Bemutató (exponenciális) forgalmazási szabályokat, annak meghatározására, tulajdonságai és példák
30. Ismételt független tesztelés. Bernoulli formula. példák
Ismételt független vizsgálatok említett tesztek, amelyek megfelelnek a következő feltételeknek:
1) Az n szám teszt során;
2) a valószínűsége, hogy egy véletlen esemény Egy az egyes tesztek állandó:
Példák újratesztelheti:
1) kitermelése több tárolóedény el, feltéve, hogy a labda után vett regisztráció színe visszatesszük a dobozba;
2) ismétlése egy shooter felvételek ugyanazon cél, feltéve, hogy a valószínűsége, hogy egy sikeres találatot kapott azonos az egyes lövés (a szerepe nullázás nem vesszük figyelembe).
Ha a valószínűségét egy esemény minden vizsgálatban állandó, akkor annak a valószínűsége, hogy az esemény bekövetkezik pontosan egyszer független vizsgálatok is :. hol.
Példa. Annak a valószínűsége, ütő a cél egy lövés egyenlő 0,7, és nem függ a lövés szám. Annak a valószínűsége, hogy 5 lövés lesz pontosan 3 ütő a cél.
Határozat. Helyettesítő a Bernoulli képlet ezekre a feladatokra kap:
31. A koncepció a központi határeloszlás tétel. A helyi és szerves Moivre-Laplace-tétel, a feltételeket az alkalmazhatóságuk. Példák.
A centrális határeloszlástétel egy tétel csoport. amelynek célja az állapotok, amelyekben van egy normális eloszlás. Ezek között tételek fontos helyet tartozik Ljapunov-tétel.
A törvény megoszlási összegek független véletlen változók (i = 1,2, \ ldots, n) „align = alsó szélessége = 147 magasság = 18 border = 0> közel van a normális eloszlás végtelen növekedést, ha a következő feltételek teljesülnek .:
minden érték véges matematikai várható értéke és szórása:
az értékek egyike sem értékének nem drámaian különbözik a többitől:
Megoldásában sok gyakorlati probléma az alábbi készítmény Ljapunov-tétel számtani átlaga a megfigyelt értékek valószínűségi változó. amely szintén egy véletlen változó (ebben az esetben a két feltétel teljesül):
ha a véletlen velichinaimeet véges matematikai ozhidaniyai diszperziós, a terjesztési
számtani, számítva a megfigyelt értékek egy véletlenszerű változó vnezavisimosti vizsgálatokban pripriblizhaetsya a normális eloszlású ozhidaniemi diszperziós, azaz,
Ezért a valószínűsége, hogy tartalmazza az intervallumban. Úgy számítható, amelyet a képlet
Használata Laplace funkció lehet írni egy kényelmes formában számítások:
Meg kell jegyezni, hogy a központi határeloszlás tétel érvényes nemcsak folyamatos, hanem diszkrét valószínűségi változók. A gyakorlati jelentősége Ljapunov-tétel hatalmas. A tapasztalat azt mutatja, hogy a törvény összeg eloszlása független valószínűségi változók, összehasonlítható szétszóródása, gyorsan közeledik normális. Még ha az időszakok számának sorrendjében tized törvénye összeg eloszlását lehet változtatni a normális.
32. * A következmények a szerves tétele de Moivre-Laplace. Példa s.
Sledstvie.Esli veroyatnostnastupleniya sobytiyav próbák állandó, és 0-tól eltérő, és 1, akkor elég nagy chislenezavisimyh teszt valószínűsége. hogy:
a) m számú előfordulásával sobytiyaotlichaetsya proizvedeniyane több, mint az összeget (abszolút értékben), azaz. ;
b) belül chastostsobytiyazaklyuchena otdo (bezárólag), azaz
c) annak chastostsobytiyaotlichaetsya veroyatnostine több, mint az összeget (abszolút értékben), azaz
Példa. A valószínűsége az esemény egy mind a 900 független kísérletek egyenlő. Annak a valószínűsége, hogy A esemény bekövetkezik: a) 710-szer; b) 710-740 alkalommal.
a) Tekintve. Ettől. a használata képletek 24-26, paritás funkciókat, és az 1. táblázatban a melléklet [4 s.553-554], kapjuk:
b) Tekintettel. Ettől. a használata képletek 27-29, a páratlan funkció és a 2. táblázat a melléklet [4, s.555], kapjuk:
Válasz: a) 0,0236; b) 0,7993.
33. A aszimptotikus a Poisson képlet és a feltételeit annak alkalmazhatóságát. Példák.
Alkalmazása Bernoulli formula nagy értékeket a termék ami egy nagyon nagy és nagyon kis számban (és), hogy rossz egy számítási szempontból, ezért van a közelítő aszimptotikus formulák.
Tekintsük a helyzetet, amikor a vizsgálatok száma a Bernoulli rendszer növeli nélkül kötött, és a valószínűségét egy esemény minden vizsgálatban nullához oly módon, hogy a termék továbbra is állandó értéket, amely jelöli. Ebben az esetben a következő összefüggés áll fenn:
Bizonyítás. Szerint a Bernoulli képlet
Mi használjuk a tény, hogy a feltétel vagy Bernoulli képlet és formáját ölti:
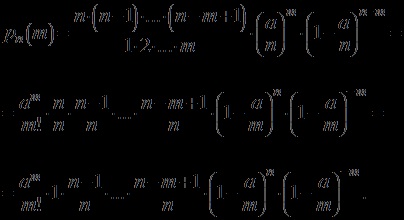
Mivel mind a rögzített, és hajlamos a végtelenbe, akkor a tényezők; ...; és törekedni egységét és a tényező hajlamos. it
Kapott Poisson-közelítés expresszióját az úgynevezett Bernoulli képlet. Ez a képlet ad jó közelítéssel a nagy és elég kicsi (például, u).
Valószínűsége az esemény abban a tényben rejlik, hogy nem lesz több idő, nyilván, ez számított képlet szerint
Példa. A vállalkozás termelt és elküldte az ügyfél 100.000 üveg sört. Annak a valószínűsége, hogy a palack lehet egy denevér. egyenlő 0,0001. Annak a valószínűsége, hogy az adminisztráció a párt lesz pontosan három vagy pontosan öt törött üveg.
Határozat. Összefüggés adja meg: n = 100000, p = 0,0001, m = 3 (m = 5).
Használata képletű Poisson
34. lemma Chebyshev. példák
A tanulmány az elmélet a valószínűség szükséges használni a koncepció egy véletlen esemény és véletlen változó. Ebben az esetben a vizsgálati eredmény előre jelzett előre, ami nem lehet bekövetkezik, vagy nem, vagy hogy egy esemény vagy egy adott érték a véletlen változó, lehetetlen, hiszen az eredmény a vizsgálati függ sok véletlen okok miatt nem azonosítható.
A tanulmány eredményeit a megfigyelések valódi véletlen tömeges jelenség, mivel vannak bizonyos mintákat. Felhívjuk a figyelmet arra a tényre, hogy az a tulajdonságuk a stabilitás. A lényege az ingatlan abban a tényben rejlik, hogy a sajátosságait az egyes véletlenszerű jelenség szinte nincs hatással az átlagos eredménye a nagy tömegű ilyen jelenségek, valamint a jellemzők véletlenszerű események és véletlen változók megfigyelték a vizsgálatok során. A korlátlan növekedés a vizsgálatok száma alig véletlen.
Tétel a nagy számok törvénye közötti kapcsolat megállapítása véletlen és szükségszerűség.
Csebisev-tétel: kellően nagy számú független valószínűségi változók X1. X2. X3. Xn. varianciája amelyek mindegyike nem haladja meg egy és ugyanazon állandó számú B, bármennyi tetszőleges kisszámú egyenlőtlenség
Ebből következik, tétel, miszerint a számtani átlag? Néhány véletlen változók növekedett a szám azt mutatja, a stabilitás a tulajdon, azaz a. E. Hajlamos a valószínűsége, hogy nem véletlenszerű értéket, amely a számtani átlagát elvárásainak ezeket a változókat, azaz valószínűsége szórása abszolút értékének számtani átlaga véletlen értékek a számtani átlaga a matematikai elvárások kevesebb mint alatt a korlátozatlan tumornövekedés az n általában 1, azaz a Gyakorlatilag bizonyos esemény.
Tekintsük a speciális esetben, Csebisev-tétel:
Tegyük fel, hogy n kísérletek n értékeket az X valószínűségi változó, amelynek az elvárás M (X) és a diszperziós D (X). A kapott értékek tekinthető valószínűségi változók X1, X2, X3. Xn,. Meg kell érteni, így van. Egy sor n elvégzett vizsgálatok ismételten. Ezért, ennek eredményeként az i-edik vizsgálat, i = l, 2, 3 n, egy tesztsorozatot jelennek kayvvvvzhdoy egy bizonyos értéket, a véletlen X változó, nem ismert előre. Következésképpen, i-e a véletlen változó értékét xi, kapott az i-edik tárgyalás, véletlenszerűen változik, ha az átmenet az egyik vizsgálati tételről tételre. Így minden érték xi lehet tekinteni egy véletlen változó Xi.
Tegyük fel, hogy a vizsgálatok megfelelnek az alábbi követelményeknek:
1) tesztek függetlenek. Ez azt jelenti, hogy az eredmények a X1, X2, X3. Xn független véletlenszerű vizsgálati-értéket;
2) vizsgálatokat végeznek azonos körülmények között, ez azt jelenti, tekintve az elmélet a valószínűsége, hogy mindegyik a véletlen változók X1, X2, X3. Xn ugyanolyan eloszlású jogot, mint a kezdeti értéke X, tehát, MXi felbontást = MX és DXi = DX, i = 1, 2 n.
Mivel a fenti feltételeknek, azt kapjuk,
Átadás a határ, mi
Az utóbbi egyenletből következik, hogy a számtani átlaga egy véletlen X változó az a tulajdonsága a stabilitás.
Csebisev-tétel van nagy gyakorlati haszna. Ez lehetővé teszi, hogy a számtani átlag, hogy képet alkothassunk a nagyságát elvárás. és fordítva. Így, valamelyik paraméter a készülék, nem felhatalmazza a rendszeres hiba lehet beszerezni egy kellően nagy számú mérés, a számtani középértéket, amely által Tétel Csebisov gyakorlatilag nem különböznek a valódi egy paraméter értékét.
Példa. Tegyük fel, hogy ennek eredményeként a vizsgált 100 független valószínűségi változók X1 kapunk. X2. ..., X100, egyenlő matematikai elvárások M (X) = 10 és egyenlő varianciák D (X) = 1. Rate valószínűsége, hogy a számtani átlaga véletlen értékek eltér az abszolút értéke a M (X) kisebb, mint 1/2.
Van egy speciális esete a Csebisev-tétel. Alkalmazása megfelelő egyenlőtlenség a valószínűsége, kapjuk: