Az ingatlan a szinusz, koszinusz, tangens, kotangens, Arkuszszinusz, Arkuszkoszinusz
Az ábra azt mutatja, az építkezés egy szinusz görbe az intervallumon.
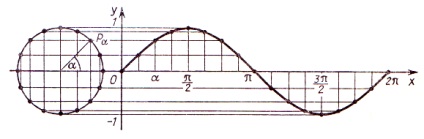
Tekintsük az alapvető tulajdonságait az y = sinx:
2) egy sor értékek a rés
3) ez páratlan funkciót. a grafikon szimmetrikus az origó körül (0, 0).
4) periodikus függvény. A legkisebb pozitív időszak
5) Funkció grafikon metszi az x tengelyen (nullák) a pontok
6) Funkció grafikon metszi Oy tengellyel (0, 0).
7) A függvény pozitív értékeket a szünetekben
8) függvény a negatív értékek az intervallumok
9) A funkció növeli az intervallumok
10) Ez a funkció csökkenti a intervallumok
11) minimális pontot:
12) maximális pontot:
13) A grafikon a függvény egy szinuszhullám
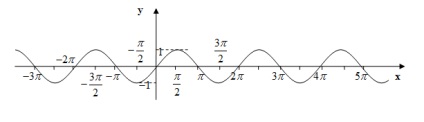
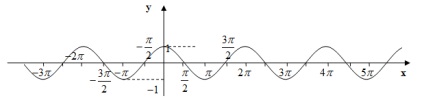
koszinusz függvény
A grafikon kapjuk a szinusz koszinusz által generált párhuzamos transzlációs olyan távolságban, hogy a bal oldalon.
2) egy sor értékek a rés
3) egy még funkciót. grafikon szimmetrikus az y tengely körül.
4) periodikus függvény. A legkisebb pozitív időszak
5) Funkció grafikon metszi az x tengelyen (nullák) a pontok
6) Funkció grafikon metszi Oy tengellyel (0, 1).
7) A függvény pozitív értékeket a szünetekben
8) függvény a negatív értékek az intervallumok
9) A funkció növeli az intervallumok
10) Ez a funkció csökkenti a intervallumok
11) minimális pontot:
12) maximális pontot:
13) A grafikon a függvény egy koszinusz
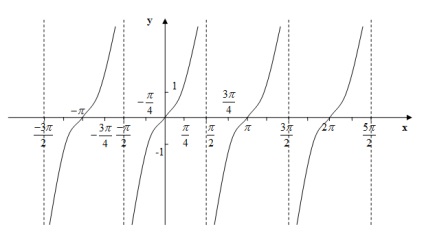
tangens függvény
3) ez páratlan funkciót. a grafikon szimmetrikus az origó körül (0, 0).
4) periodikus függvény. A legkisebb pozitív időszak
5) Funkció grafikon metszi az x tengelyen (nullák) a pontok
6) Funkció grafikon metszi Oy tengellyel (0, 0).
7) A függvény pozitív értékeket a szünetekben
8) függvény a negatív értékek az intervallumok
9) A funkció növeli az intervallumok
10) csökkenő rések hiányoznak.
11) nincs minimális pont.
12) a maximum pont nincs.
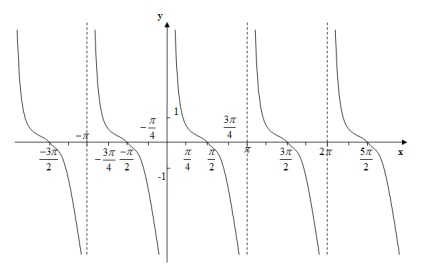
13) A grafikon a függvény tangensoida:
kotangens függvény
3) ez páratlan funkciót. a grafikon szimmetrikus az origó körül (0, 0).
4) periodikus függvény. A legkisebb pozitív időszak
5) Funkció grafikon metszi az x tengelyen (nullák) a pontok
6) A funkció nem metszi a tengelyt Oy.
7) A függvény pozitív értékeket a szünetekben
8) függvény a negatív értékek az intervallumok
9) A függvény nem növeli a időközönként.
11) nincs minimális pont.
12) a maximum pont nincs.
13) A grafikon a függvény kotangensoida:
időszak jellemzői
1) Ha T - a bázis időszak függvény y = f (x). a szám a fő időszak az y = f (ax). ahol a - bármilyen pozitív szám.
2) Ha egy periodikus függvény y = f (x) és y = g (x) azonos időszakban T, akkor az összegük, különbség és a termék is van egy időszak T.
3) Ha egy periodikus függvény y = f (x) és y = g (x) összehasonlítható időszakok T1 és T2. van egy közös időszakban.
4) Az az időszak egy összetett függvény y = g (f (x)) egybeesik azzal az időszakkal, a függvény y = f (x).