Algoritmusok és adatszerkezetek kezdőknek bináris keresési fa
Eddig néztem az adatszerkezetet, az adatokat, hogy vannak elrendezve lineárisan. A láncolt lista - az első csomópont egy utolsó. A dinamikus tömb - formájában folyamatos blokk.
Ebben a részben megnézzük egy teljesen új adatstruktúra - fa. Pontosabban, a bináris (binary) keresési fa (bináris keresési fa). Binary keresési fa egy fa szerkezetű, de az elemek benne vannak elrendezve bizonyos szabályok szerint.
Először is vizsgáljuk meg egy normális fa.
Fa - egy olyan struktúra, amelyben minden egyes csomópont lehet nulla vagy több részegységek - „gyermek”. Például egy fa a következőképpen nézhet ki:
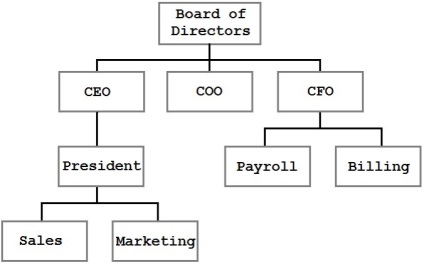
Ez a fa szerkezetét mutatja a cég. Csomópontok jelentik az egyének vagy egységek, vonal - összeköttetések és kapcsolatok. Fa - ez a leghatékonyabb módja a bemutató és az említett információk tárolására.
Binary keresési fa
Binary keresési fa hasonló a fa például a fenti, de megépíteni bizonyos szabályok szerint:
- Minden csomópont nem több, mint két gyerek.
- Bármilyen érték alacsonyabb, mint az a csomópont lesz a bal gyerek a bal gyermek vagy a gyermek.
- Bármilyen érték nagyobb vagy egyenlő a csomópont lesz a jobb gyermek vagy a gyermek joga a gyermek.
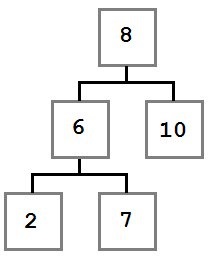
Nézzük meg egy fát, épült szerint ezek a szabályok:
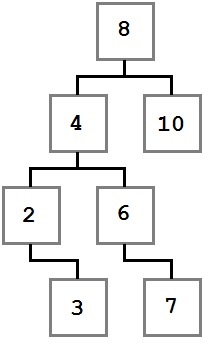
Binary keresési fa
Figyeljük meg, hogy ezek a korlátozások érintik a faszerkezet. Minden érték marad a gyökér (8) kevesebb, mint nyolc, minden értéket a jobb oldalon - nagyobb vagy egyenlő, mint a gyökér. Ez a szabály vonatkozik a csomópont a fa.
Ezt szem előtt tartva, képzeljük el, hogy hogyan lehet építeni egy fa. Mivel az első fa üres volt, az első hozzáadott érték - nyolc - volt gyökere.
Nem tudjuk pontosan, milyen sorrendben a többi hozzáadott értékeket, de jelentheti az egyik lehetséges módja. A csomópontok adunk az Add módszerrel. amely megkapja a hozzáadott érték.
Nézzük meg az első lépéseket.
Először hozzáadott 8. Ez az érték lesz a gyökér a fa. Ezután add 4. Mivel 4 kevesebb, mint 8, rakjuk be a bal oldalon a gyermek szerint a szabály 2. Mivel csomópont nyolc nem engedélyezte a gyermekek, a 4. az egyetlen gyermek maradt.
Ezután adjunk hozzá 2 2 8-nál kevesebb, így megyünk a bal oldalon. Mivel a bal már egy értéket, hasonlítsa össze a behelyezett. 2 kevesebb, mint 4, és négy gyermek nélkül maradt, így válik a 2 bal gyermek 4.
Ezután adjunk hozzá az első három. Odamegy a bal oldalon a 8. és 4. Mivel azonban a 3 nagyobb, mint 2, ez lesz az a gyermek jogairól 2. szerint a harmadik szabály.
A szekvenciális összehasonlítás betétek potenciális szülő addig folytatódik, amíg, amíg meg nem találja a helyét, hogy helyezze be, és megismételjük az egyes plug-számít, amíg nem minden az egész fa kerül kialakításra.
osztály BinaryTreeNode
Távolítsuk módszer
- Viselkedés: Eltávolítja az első csomópontból egy előre meghatározott értéket.
- A komplexitás: O (log n) átlagosan; O (n) a legrosszabb esetben.
Törlése csomópontot a fa - az egyik ilyen műveletek egyszerűnek tűnhet, de valójában tele van sok veszélyt rejt magában.
Általában az algoritmus törlése az elem a következő:
- Keresse meg a csomópont, amely a törölni kívánt.
- Távolítsa el.
Az első lépés nagyon egyszerű. Úgy véljük, a keresés Tartalmazza csomópont a módszert. Amint megtaláltuk a helyszínen, hogy el akarja távolítani, van három lehetséges esetet.
1. eset: A törölt csomópont nincs joga gyerek.
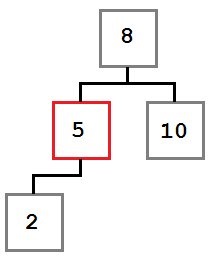
Ebben az esetben, egyszerűen mozgatni a bal gyermeke (ha van ilyen) az a hely, a törölt csomópont. Ennek eredményeként, a fa így néz ki:
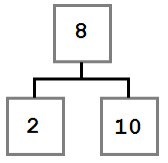
2. eset: A törölt csomópont csak a megfelelő gyermek, ami viszont nem a bal gyerek.
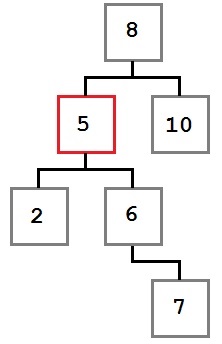
Ebben az esetben meg kell mozgatni a jogokat a gyermek csomópont kell hagyni (6) a helyén. Eltávolítása után a fa fog kinézni:
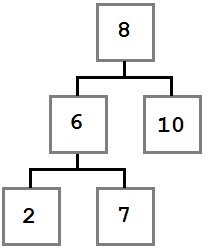
3. eset: A törölt csomópont az első gyermek, aki egy bal gyerek.
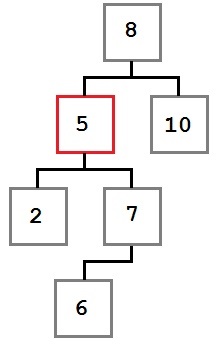
Ebben az esetben helyezze az eltávolított csomópontot foglal a bal szélső gyermek a jobb gyermek csomópont el kell távolítani.
Lássuk, miért van ez így. Ismerjük részfájának kezdve a csomópont el kell távolítani az alábbiak szerint:
- Minden érték a jobb nagyobb vagy egyenlő, mint az érték a csomópont.
- A legalacsonyabb érték a jobb részfa - balra.
Mi életbe dozhny törölt csomópont értéke kisebb vagy egyenlő a csomópont a jobb oldalon. Ehhez meg kell találnunk a legkisebb érték a jobb részfa. Ezért itt is a bal szélső csomópontja a jobb részfa.
Eltávolítása után a Csomópontfa fog kinézni:
Most, hogy tudjuk, hogyan kell törölni csomópontokat, nézd meg a kódot, amely megvalósítja az algoritmust.
Megjegyezzük, hogy FindWithParent módszerrel (lásd. A Tartalmazza módszer) visszatér talált csomópont és a szülő, mert van, hogy cserélje ki a bal vagy a jobb gyermek szülőcsomópont távolítani.
// Ha a szülő érték nagyobb, mint a jelenlegi,
// Jobb gyermeket az aktuális csomópont lesz a bal gyermek a szülő.
szülő. Bal = áram. Jobb;
else if (eredmény <0 ) >> // 3. eset: Ha a jogai a gyermek gyermek maradt, a bal szélső gyermek a jobb részfa // helyettesíti a törölt csomópont. más // A bal részfa jobb részfa a szülő válik a bal szélső csomópontot. leftmostParent.Left = leftmost.Right; // Bal és jobb gyermeke az aktuális csomópont lesz a bal és jobb oldalán a bal szélső gyermek. leftmost.Left = current.Left; leftmost.Right = current.Right; ha (szülő == null) <_head = leftmost;> más
// Ha a szülő érték nagyobb, mint a jelenlegi,
// bal szélső csomópont lesz a bal gyermek a szülő.
szülő. Bal = bal szélső;
Mozgás fák
Bejárás a fa - egy család algoritmusok, amelyek lehetővé teszik, hogy feldolgozza minden csomópont egy bizonyos sorrendben. Minden bypass algoritmusok alábbiakban példaként kell használni a következő fa:
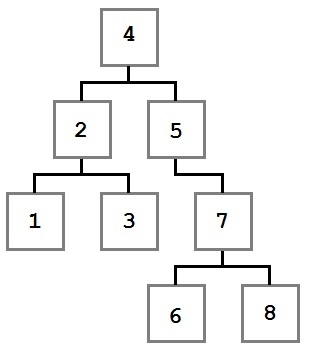
Példa fa bypass
megoldásokat példákban elfogadja paraméter Action
Továbbá, kivéve a leírását a viselkedés és algoritmikus módszer bonyolultsága utalják a rendelést kapott értékek feltérképezése során.
Előrendelés módszer (vagy előtag bypass)
- Viselkedés: elmozdulási a fa prefix érdekében végezze el az alábbi lépéseket minden csomóponton.
- A komplexitás: O (n)
- Bypass eljárás 4, 2, 1, 3, 5, 7, 6, 8
Amikor előtag bejáráshoz megkapja az aktuális érték a csomópont előtt, az első lépés a bal részfa, majd jobbra. Kezdve a gyökér, először azt, hogy az érték a 4. Ezután ugyanúgy kerülni a bal gyermek és a gyermek, majd a jobb oldali gyermek és minden gyermekének.
Az előtag általában használják, hogy megkerülje példányt fa tartósítására felépítését.