Abstract ókori görög tudós és matematikus Archimedes

Ha minden felsorolt újabb amely által Archimedes mechanika, nyilvánvaló lesz, hogy a csodálkozás és a tisztelet, amellyel ő kortársai, és most is mindazoknak, akik közel állnak a matematika, mechanika és alkalmazott tudományok.
Hódítja és nagy erkölcsi Arkhimédész. Ő egy igazi hazafi az ő városa. Ha kemény nap Syracuse és római seregek parancsnoksága alatt Marcellus ostromolták a várost két oldalról, és egyik sem az ostromlott nem reménykedett az üdvösségre, az akkor volt, és vezette Archimedes működtetett gépek, jóval azelőtt építettek.
„Az ellenséges gyalogság söpörte őket lövése pár személyes jellegű nyilak és kövek hihetetlen nagyságú, a zaj és a rettenetes sebességet. Határozottan, semmi sem hozza az erejét hatásukat; azok felborult akikben estek, és csalódott a soraiban. A tenger hirtelen emelkedett a falakon át a hajónaplót, görbe szarvak a hasonlóság. Egyikük ütött a tetején egy kis hajók és erő hatása megfulladtak; Más vas la PAMI vagy csőr, mint Crane, megragadta az orrukat hajók, emelte a levegőbe, tegye a hajó farában, majd megfulladt. Gyakran a hajó emelkedik magasan a tenger felszínét, és lóg a levegőben, ő rázta a döbbenet mások más-más irányba, bemutatva a szörnyű látvány, amíg a személyzet nem tisztázott, vagy lő. Sambuca, egy gépet, Marcellus már hozott egy pár hajó, és vezette a falra. még messze még nem volt ideje, hogy megközelíteni őket, egyrészt azért, mert levette a súlya egy kő tíz tálentom, majd újabb és újabb. Úgy esett az autó egy szörnyű zaj, és a teljesítmény, összetört teste szakadt, anyák uni Nos kommunikáció, így a Marcellus, nem tudta, mit tegyen, úgy döntött, hogy vitorlázni a flotta gyorsan és elrendelte, hogy a gyalogság visszavonulni. de a nyilak, és felzárkózik velük, beleesett visszavonuló, úgy, hogy súlyos veszteségeket szenvedett. Marcellus még sikerült elkerülni a veszélyt. Tréfálkozott felett technikusok és mérnökök, és azt mondta: „Én nem áll le, ha küzdünk a matematikus? Ott ült a fal mögött spo Coyne, megfullad hajóinkat, és dobott minket újra annyi nyilak, hátrahagyja a mitikus száz rukih óriások. Sőt, az összes többi Shiraki Zena szolgált egyfajta Archimedean test gépek, egy lélek volt, hogy minden mozog, minden irányított lyala: „(Plutarkhosz).

Plutarkhosz azt írta: „Ő egyedül volt otthon, alapos megfontolás geometriai rajzokat. Mint minden megértés és érzések mélyen a gondolataiba, nem figyelni a zaj és a sír a rómaiak, a tolvaj vavshihsya a városban. Hirtelen megjelent előtte egy római katona. Archimedes már csak kiabálni: „Ne nyúlj a rajzok -szerű kard katona megütötte.”
Összefoglalva azt szeretném idézni Plu Tarkh mélysége geometriai helyzetét Archimedes.
„Az összes tétel a geometria nem nehezebb és mélyebb, mint Arkhimédész tétele.
Magam mindig azt hittem, mikor első jelei milsya az ő matematikai állítások, amelyek nehezen előtt, hogy az emberi elme nem képes bizonyítékot találni őket. Azonban, ha tudod, hogyan Archimédesz maga bizonyítja őket, úgy érzi, mintha te magad találtam ezt a bizonyítékot - mielőtt ez egyszerű és könnyű. "
nagy felfedezések Arkhimédész
Az esszét „parabola négyszögesítése” Arkhimédész bizonyult kiszámításának módszerét a területet a parabolikus szegmens, és tette több mint kétezer évvel felfedezése előtt az integrálszámítás. Művében: „A mérési kör” Archimedes első kiszámított számú „pi” - aránya kerülete az átmérő - és bebizonyította, hogy ez ugyanaz minden körben. Mi továbbra is használhatja a rendszert találta Archimedes nevek egészek. Néhány síkgeometria tételek először bizonyítja Archimedes. Tehát, a téren tétel háromszög nick három oldalán
mondta nevű képlet Heron-képlet, mert neki tulajdonítják a széles körű alkalmazását a gyakorlatban.
tulajdonított Heron, ez volt az első által javasolt Arch-méz. A matematikai módszer Arkhimédész kapcsolódó matematikai munka a pythagoreusok és teljes munkájukat Euclid és Archimedes kortársak felfedezések, legyen az a tudás fizikai tér körülöttünk, hogy a tudás az elméleti tárgyak alakjához, amely ebben a tér, a forma tökéletes geometriai formák, a amely tárgyak többé-kevésbé szoros és a törvények, hogy meg kell tudni, hogy ha azt akarjuk, hogy befolyásolja a fizikai világban. De Archimedes is tudta, hogy a tárgyak nem csak a forma és méret: mozognak, vagy áthelyezhetjük vagy helyben maradnak az intézkedés bizonyos erők, amelyek mozgatni a dolgokat előre, vagy hogy egyensúlyba hozza. Nagy sirakuzets tanulmányozta ezeknek az erőknek, feltalálás egy új ága a matematika, ahol az anyagi testek, mivel azok geometriai forma, tárolja, ugyanakkor annak súlyosságát. Ez a súly a racionális geometria és a mechanika a statika és hidrosztatikai, az első törvény, amely megnyitotta Archimedes (törvény

Ezt követően ezek a mechanizmusok már széles körben használják szerte a világon. Érdekes, hogy a továbbfejlesztett változata a víz daruk megtalálható elején a XX században a kolostor található Valaam, az egyik az északi szigetek a magyar. Ma archimedesi csavar használják, például a közönséges daráló. A találmány egy csiga oda vezetett, hogy egy másik fontos találmány, még ha ez vált általánossá - a csavar a találmány épített egy csavarral és anyával. Azok honfitársaik, akik tekinthető semmisnek ilyen találmány Archimedes bemutatott erős bizonyíték az ellenkezőjére, a nap, amikor ügyesen beállítani a kart csavar és csörlő, talált eszközöket, hogy a meglepetés bámészkodók, indult egy nehéz gálya sodort, minden a személyzet és a rakomány. Még több meggyőző bizonyíték engedett 212 BC.
Puzzle megoldások
1. Dana kör, amelynek a sugara vesszük 1. Hozzuk létre az a körök száma, koncentrikus vele, így a kapott gyűrűk voltak egyenlő részre
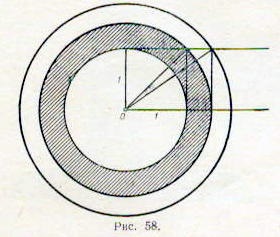
közte és a terület mindegyikének egyenlő lenne a kisebb területen egy kör (ábra. 58).
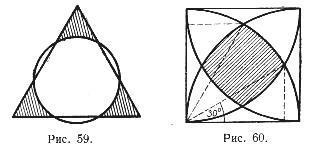
2. A párt egy szabályos háromszöget. A központ a sugara a / 3opisana kört. Határozzuk meg a háromszög területe kívül fekszik a kerülete mentén (lásd. 59.).
3. központok négy körrel található egy négyzet sarkaiban az oldalsó a. A sugarak a körök minden rendben. Számítsuk ki a terület része a sík közös a köröket (ábra. 60).
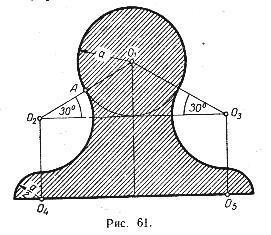
4. Find területén (ábra. 61), ha A = a 01.
A szám π 2.
A szegmens AB átmérőjű össze egy félkört-Ness (ábra. 62) elosztjuk az AB szakasz felét minden
másfélszer átmérőjű konstrukció egy félkör-Ness, forgalomba őket ellentétes oldalán AB. ezek
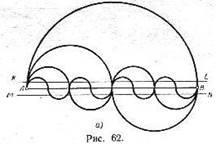
két félkör összege hullámos vonal hossza tól B jelentése megegyezik az eredeti hosszát a félkör. Most osztani a szegmens AB négy egyenlő részre, és össze egy hullámos vonal az Állandó a négy félkörök, az azonos teljes hossza π * AB / 2. Mi továbbra ez a folyamat a végtelenségig, elosztjuk szegmens AB 8, 16 egyenlő részre, és számukra egy félkört, váltakozva elrendezett egyik és a másik oldalon a vonal AB fog fordulni egy szekvenciát hullámzó vonalak, szorosabban közelíti a szegmens AB és miután őt, mint a pre- üzlet. Sőt, mivel nem volt egy keskeny sávban, a kifizető által közvetlen hívás KL és a MN, párhuzamos AB, tsya talált egy ilyen hely a mi egymás után, amelyben az összes hullámos vonal teljes hosszában A-ból B teljes mértékben illeszkedik a zenekar. De a hossza az összes hullámos vonalak azonos és egyenlő tc * AB / 2. Az ilyen kell lennie az azonos hosszúságú határa ezeket a sorokat, azaz AB szakaszt a egyenlőség
F. Rudio, A kör négyszögesítése, GTti 1934.
VP Scheremetevsky, Tanulmányok a matematika története, Uchpedgiz 1940.
S. Ya. Lure, Archimedes, Szovjetunió Tudományos Akadémia, 1945.
SN W Rae falu, három ősi geometria problémát. A tapasztalat a tanórán kívüli tevékenységek matematikai középiskolás Uchpedgiz 1955.
VI Lebedev, Tanulmányok a történetét az egzakt tudományok, Vol. 4 Híres feladat ókor, M. 1917.
Hála az alkotók a honlapon! Vegyünk egy kis szünetet, diák szórakozni: A pályázó, aki arról álmodott, hogy orvos, nem felelt meg a felvételi vizsgák, és a következő évben az lesz, hogy álma válik egy általános. By the way, az anekdota veszünk chatanekdotov.ru