A vetítés vektorok
Fizika - a tudomány a természet a legáltalánosabb értelemben. Tanulmányozza a különböző substatsii lény (anyag, anyag kitölteni) és legegyszerűbb formája a mozgás, valamint az alapvető kölcsönhatások. természet, mozgásának ellenőrzésére a kérdésben.
Mechanics - a fióktelep a fizika, tanul. mozgása anyagi testek, és a kölcsönhatás közöttük.
Kinematikája - egy része a mechanika, hogy tanulmányozza a matematikai leírása a mozgás szervek vizsgálata nélkül okainak mozgás.
Dynamics - részben a mechanika, hogy a tanulmányok okainak mechanikus mozgást.
Alapvető elméleti modellek valódi testek anyagi pont - van egy csomó, de nem a méret;
merev test - a hangerőt a véges méretű, teljesen kitöltve az anyaggal, a távolság bármely két pont között a közeg töltési térfogata nem változik mozgás közben
1.1 A skalár - fizcheskaya értéket. amely esetben csak az értéket.
Vektor - fizcheskaya értéket, amely meghatározza nemcsak érték, hanem az irányt.
Geometriailag vektor képviseli, mint egy irányított vonal szegmens, amely egy skála hossza - a vektor egység.
Egy vektor mennyiséget jelöli egy megfelelő fizikai mennyiség egy nyíl rajta: .Modul vektor jelölése nélkül nyilak: | | vagy V.
Bármilyen vektor felírható összege több vektorok.
Cseréje egy vektor a vektor összege több más úgynevezett bővítése a vektor komponensek. Vektor alkatrészek, természetesen, szintén vektorok. A bomlás a vektor komponensek képes végtelen számú módon, mint bármilyen skalár mennyiség bővíthető végtelen számú módon szempontból.
Leggyakrabban termelnek bomlás vektorok irányban a tengely egy derékszögű koordináta-rendszer meghatározott. Kiválasztásával egy adott koordinátarendszerben lehet jellemezni egy vektor nagyságát és előjelét annak elemei, nem mutatva az irányt.
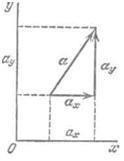
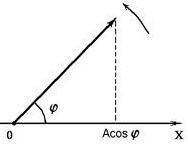
Érték komponens venni annak jele, az úgynevezett projekciós vektor irányában a mindenkori tengely egységet vektor - vektor. abszolút értéke, amely az egység.
Egység vektorok gyakran jár együtt a koordinátatengelyek a koordináta-rendszer (különösen a tengelyei egy Descartes-féle koordináta-rendszer). Az irányok Ezen vektorok egybeesik az irányokat a megfelelő tengelyekre, és gyakran már egybeesik a kezdete a koordináta-rendszer.

1.3 Kiegészítés Vectra
Grafikus összeadás és kivonás. Szabályok és parallleogramma háromszög. kivonása vektorok
Analitikai módszer az összeadás és kivonás

Szabály szünet - közel törte fel a sokszög.
1.4 Szorzás vektorok

1.4.1 1.4.2 1.4.3 1.4.4 1.4.5
vektor termék egy vektor kereszt terméket vektorovi
Transzformációs vektorokat nyírás:
= +. X = ax + x 'y = Ay + y' ... forgatása közben. X = h'cosa - y'sina, y = x'sina + y „cosa
upon inverziós. x = -x 'y = -Y' ... = pseudovectors axiális - koordinátákat után reverzibilisek invertálása koordinátarendszerek
vektor = true poláris - koordinátát nem változott az inverzió koordináta-rendszer
7.Skalyarnym termék dvuhvektorov egy szám egyenlő a termék a modulusok ezeknek koszinusz vektorok
Fizikából ismert, hogy a munka, ha mozgó erő F S = F S • • cosj m. F. = A (F • S).
Deriváltja az f (x) x0 a határ aránya növekmény Af funkció ezen a ponton, hogy a növekmény Ah érv, amikor az utóbbi nullához (végtelenül kicsi). Meg van írva, mint. LimΔx → 0 (Af (x0) / Ax) = limΔx → 0 ((f (x + Ax) -
származék. A származék x pontban 0 egyenlő a lejtőn a érintő a függvény grafikonját y = f (x) ezen a ponton.
8.Vektornym vektor termék a
vektor olyan vektor, amely a következő tulajdonságokkal rendelkezik: A hossza megegyezik
C vektor merőleges a síkra, amelyben fekszenek az a és b vektorok
Vektor van irányítva, oly módon, hogy a forgása vektorak vektoruosuschestvlyaetsya óramutató járásával ellentétes, ha
a végéről nézve a vektor (ebben az esetben, azt mondja, hogy a hármas vektorovi - jobb).
Vektor termék megegyezik a terület a paralelogramma épített a vektorok
9.Smeshannym termékét három vektor
, egy szám egyenlő a vektor termék,
szorozva a vektor.
A kevert termék térfogatával egyenlő a paralelepipedon épített a vektorok
Integral - az egyik legfontosabb fogalom a matematika, amely abból adódott kapcsolatban, hogy szükség van, egyrészt, hogy megtalálják a funkció származékai (például találni egy függvényt, amely kifejezi az útnak egy mozgó pontot, ezen a ponton a sebesség), és a másik - mérésére terület, térfogat , ívhossz, a munka erő egy bizonyos ideig, stb integráció - .. a folyamat találni az integrál.
Primitív funkció - egy funkciót, amely egy származéka Ez a funkció a teljes domain. A határozatlan integrál függvény - a készlet minden primitívek egy adott funkciót.
Határozott integrál egy folytonos függvény egyenlő az értékek közötti különbség a határozatlan integrál a felső és alsó határértékek.
A geometriai jelentése a határozott integrál. Ha f (x)> 0
[a, b], az integrál terület ívelt ABCD trapéz.
2.1 A koncepció a származék és differetsiala skalárfüggvény egyváltozós.





Három módon a mozgás feladatokat.
A pont pozíciója tekintetében otschѐta rendszer (O), zadaѐtsya rádiuszvektorhoz, az elejétől provedѐnnym otschѐta mielőtt pont M.
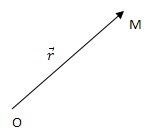
A törvény a mozgás zadaѐtsya vektor egyenlet:
Ha a koordináta így pont helyzetét zadaѐtsya bármely három koordinátákat.
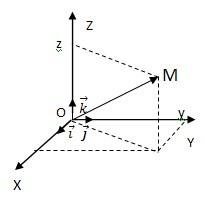
Ha kiválaszt egy Descartes-féle derékszögű koordináta-rendszer, a törvény a mozgás a lényeg M zadaѐtsya három egyenletet:
Ezt a módszert alkalmazzák, általában, ha ismert röppálya pont képest a kiválasztott rendszer otschѐta.
A pont pozíciója M határozzuk meg a távolságot
választott pályája kezdetét otschѐta mérve a pálya mentén, és megteszi az alkalmazandó jogot. A törvény a mozgás zadaѐtsya egyenlet
.
Röppálya - egy folyamatos vonal, amely leírja a ponton svoѐm mozgás. Az egyenlet a pálya lehet beszerezni a kinematikus egyenletek a mozgás, kivéve egy alkalommal. röppálya egyenlet az a pontok koordinátái:
.
Mozgó - vektor provedѐnny a kezdeti helyzetben, hogy a végpont.
Az expressziós vektor halad át a növekmény a sugár vektor és a koordinátákat
;