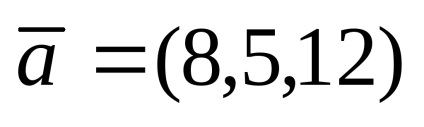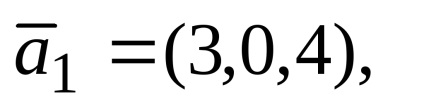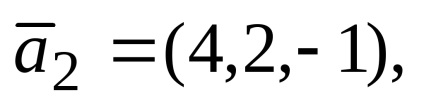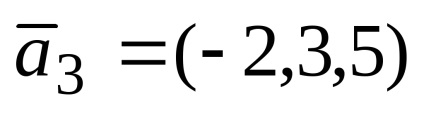A vektorok n-dimenziós térben
n-dimenziós vektor aritmetikai
számtani n-dimenziós vektor egy rendezett halmaza n valós számok és a számok szerepelnek ebben az úgynevezett vektor koordinátáit.
A komponensek száma a vektor neve a dimenziója.
Ha minden koordináta a vektor nulla, az úgynevezett nulla vektor, és jelöljük 0 vagy

Ha a megfelelő koordinátákat iravny vektorok, a vektorokat nazyvayutsyaravnymi:
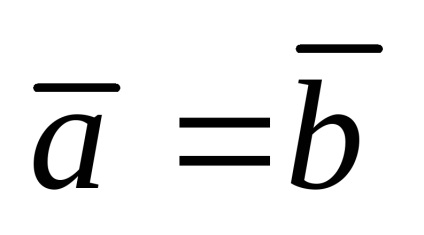

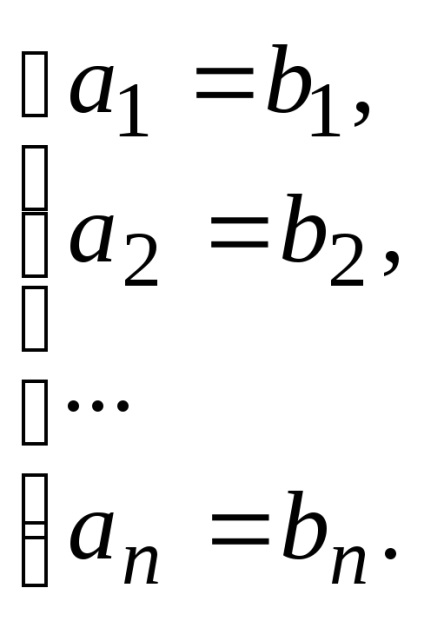
A legegyszerűbb műveletek n-dimenziós vektorok vektor összeadás, kivonás és szorzás a vektorok a vektor egy szám. Az ilyen műveletek nevezzük lineáris. Összeadni és kivonni vektorok lehet csak azonos méretű.
Sum (különbség) két n-dimenziós vektorok inazyvaetsyan dimenziós vektort
Proizvedeniemn dimenziós vektor számos

.
Így, azzal a kiegészítéssel, vagy kivonásával vektorok, vagy eltávolításakor azok ugyanazokkal a koordinátákkal. Ha megszorozzuk minden vektor számos koordinátája vektor szorozni ezt a számot.
Az n-dimenziós vektorok, ahol a belépett a műveletek összeadás, kivonás és szorzás vektor nevezett szám az n-dimenziós vektortér és számtani jelöljük
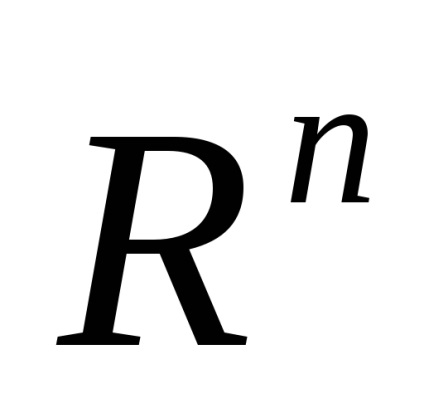
A lineáris függőség a vektorok
Legyen mn-dimenziós vektorok
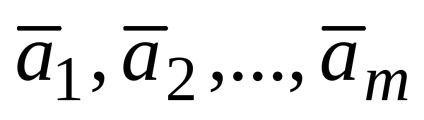
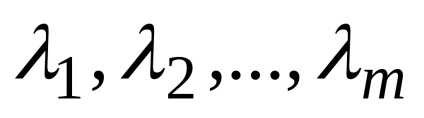
Ez az úgynevezett lineáris kombinációjával a vektorok
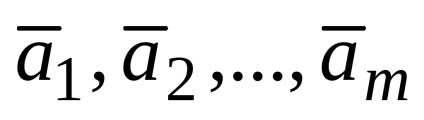
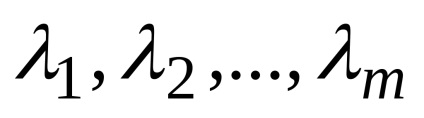
Lineáris kombinációja n-dimenziós vektorok szintén egy n-dimenziós vektor.
vektorok
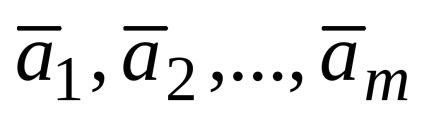
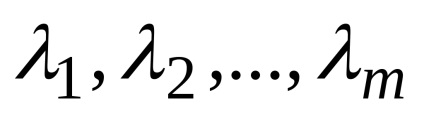
.
Ha ez az egyenlőség csak akkor lehetséges, ha az összes számot
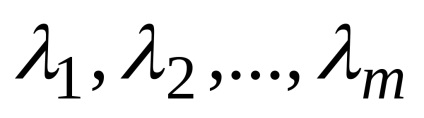
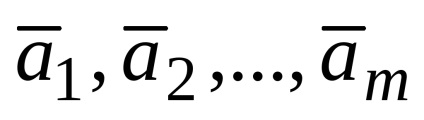
megfontoltabb vektorok
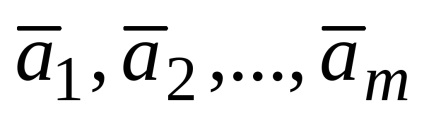
Ha egy vektor

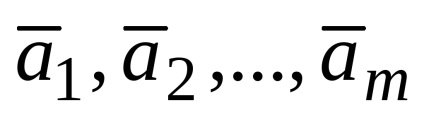
,
kiterjesztette a rendszer vektorok lineárisan függ. Ezzel szemben, ha a rendszer vektorok
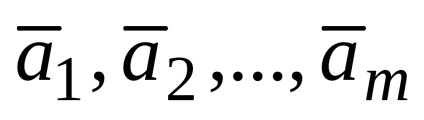
Így az a feltétel, lineáris függőség a vektorok az alábbiak szerint történik: a rendszer vektorok lineárisan függ, ha, és csak akkor, ha legalább az egyik rendszer vektorok egy lineáris kombinációja a más vektorok.
Basis vektorok és rang rendszer
Adott egy rendszer vektorok
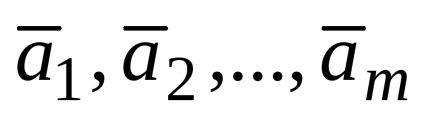
vektor rendszer lehet több bázisok. Ebben az esetben ezek mindegyike azonos számú vektorok.
A rangsorban a rendszer vektorok száma vektorok bármely rendszer alapján. Más szóval, a rangot vektorok egyenlő a maximális számú lineárisan független vektor rendszer.
Bazisomn dimenziós vektortér egy sor n lineárisan független vektor ebben a térben.
Vektor bomlása a rendszer vektorok
Legyen egy olyan rendszer, vektorok
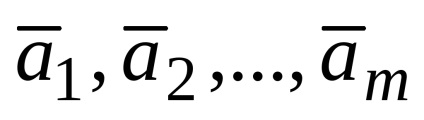
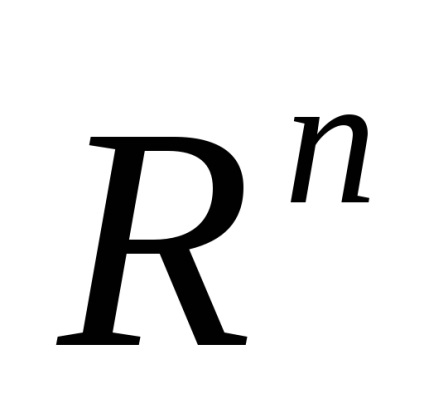
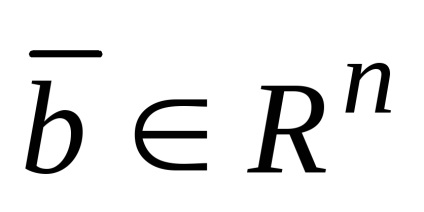
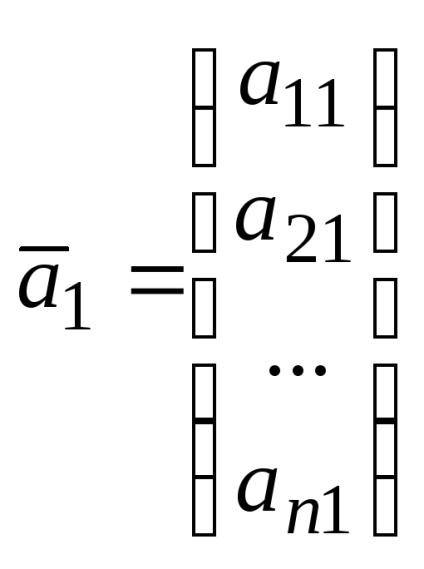
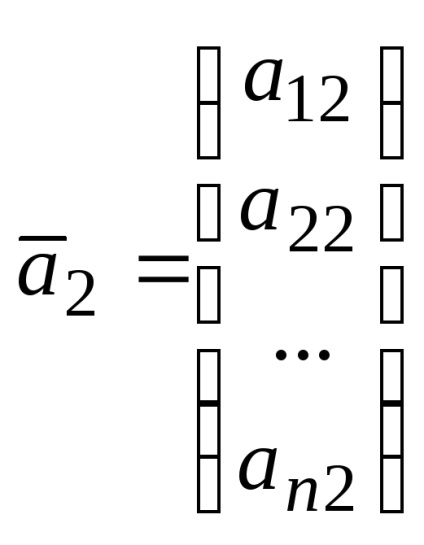
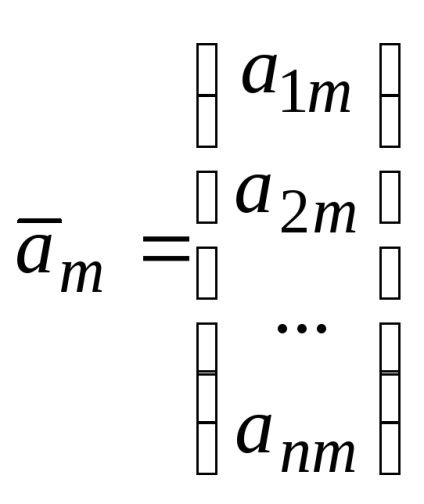
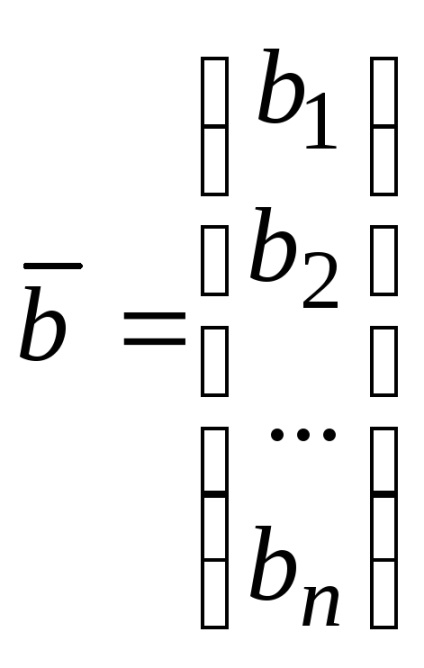
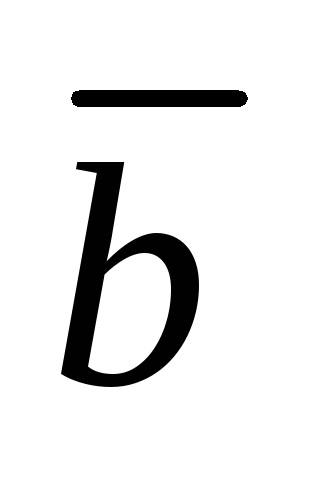
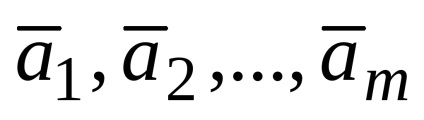
.
Ez a rekord az úgynevezett vektor bomlás
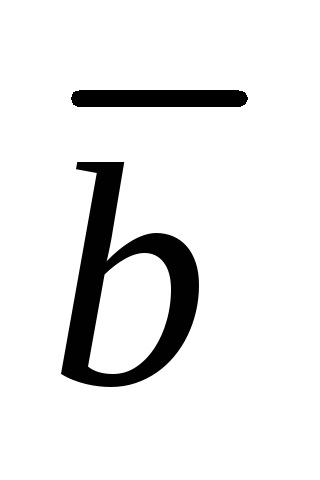
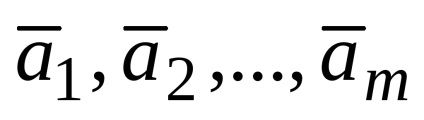
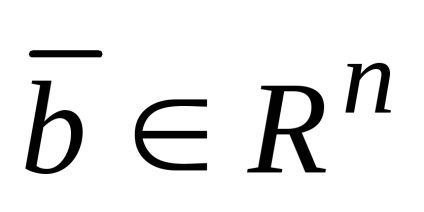
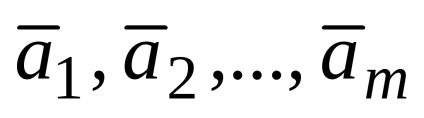
Írunk ezt formájában lineáris kombináció:
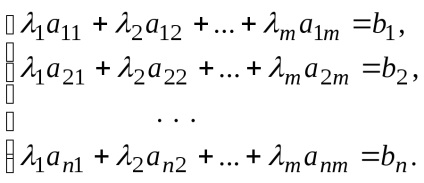
A rendszer n egyenletek m változók
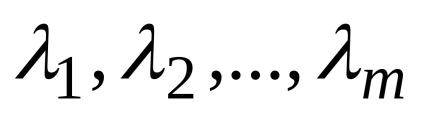
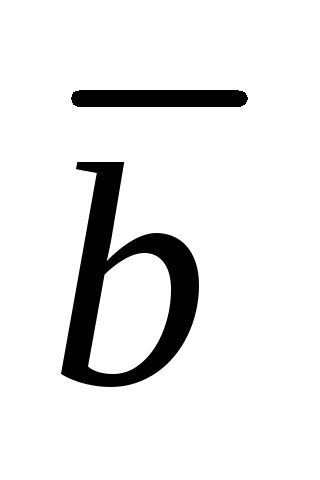
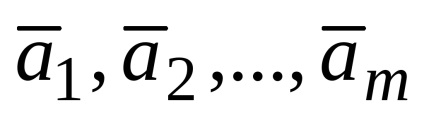
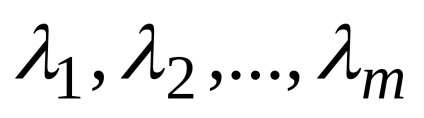
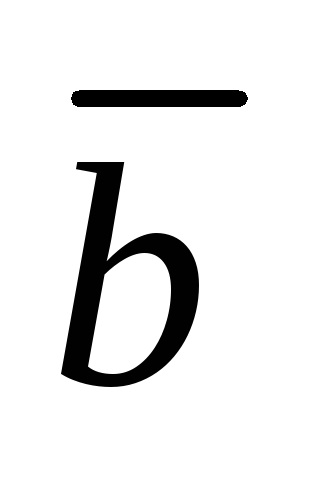
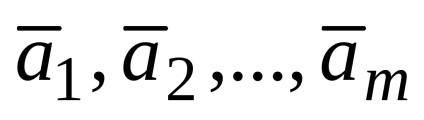
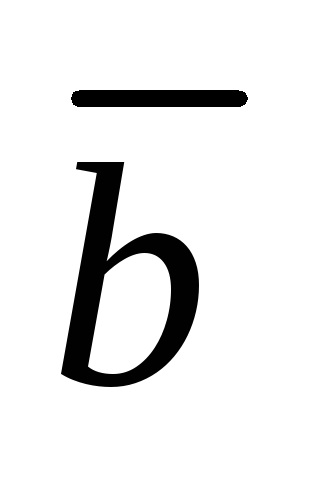
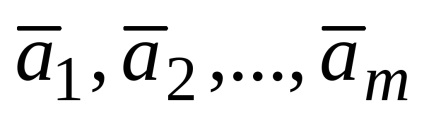
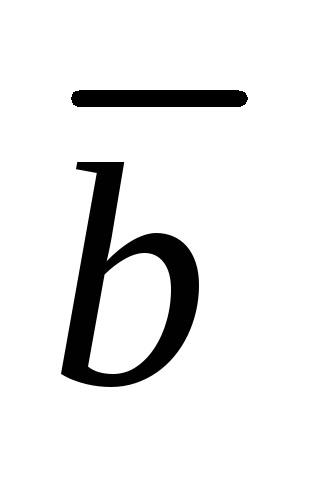
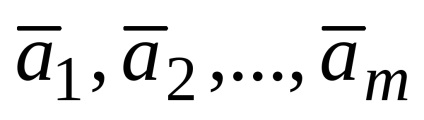
Így a ábrázolása a vektor lineáris kombinációjával vektorok egyenértékű megoldani egy lineáris egyenletrendszer.
Hagyja, hogy a vektorok
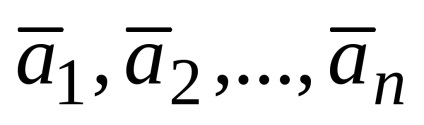

1. példa. adott vektorok
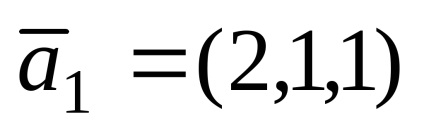
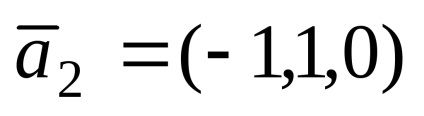
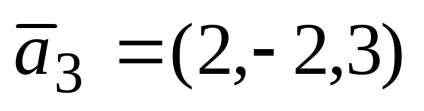
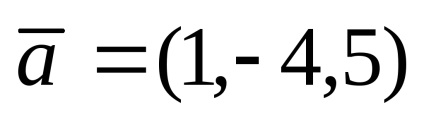
Határozat. Azzal a feltétellel, hogy a vektor probléma

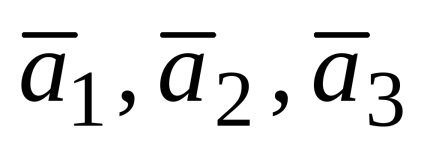
A rendszer három egyenlet három változóval
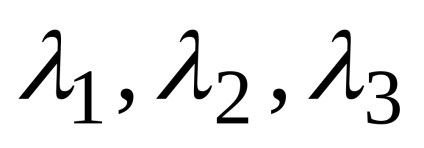
Kérdések önismereti
Az úgynevezett n-dimenziós vektor számtani?
Által meghatározott összege a különbség a két n-dimenziós vektorok, és a terméket n-dimenziós vektor egy skalár?
Mi egy lineáris kombinációja a vektorok m?
Mi a rendszer vektorok hívják lineárisan függő és lineárisan független?
Mit jelent a bomlás a vektor vektorok a rendszer?
Mi a neve alapján a rendszer és az alap vektorok a tér?
Feladatok az önálló munkavégzésre
Vannak vektorok alapot a kétdimenziós térben. bomlik vektor
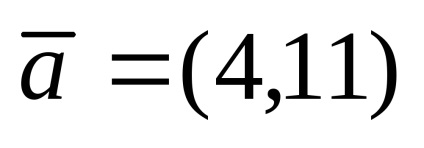
bomlik vektor