A tulajdonságait konvex halmazok
A konvex halmaz - részhalmaza euklideszi tér tartalmazó összekötő szakasz bármely két pont bármely sokaságának.
Más szóval, a készlet az úgynevezett konvex, ha:
Azaz, ha X együtt bármely két pont, amelyek ehhez a szett tartalmaz egy összekötő szakasz őket:
.
A térben konvex halmazok egyenes, félhosszú az intervallum, egy ponthalmaz.
A konvex tér a tér maga, vagy annak bármely lineáris altér, labda, vágás, egypontos készlet. Szintén kiemelkedő olyanok készletek:
- egyenes. ponton áthaladó 0 x irányú vektor h:
;
- gerenda. áradó pont x 0 irányába a vektor h:
;
- hipersíkot H p? A normál p:
;
- fél-hipersíkot amely osztja a teret:
,
.
Mindezek a készletek (amellett, hogy a golyó) egy speciális esete a több konvex poliéderek.
A tulajdonságait konvex halmazok
- A kereszteződés konvex halmazok konvex.
- Egy lineáris kombinációja több pontot a konvex konvex.
- A konvex halmaz bármely konvex kombinációja a pontokat.
- Bárhol az n-dimenziós euklideszi térben konvex burka a készlet is képviselteti magát egy konvex kombinációja legfeljebb n + 1 pont ez a készlet
Tekintsük n - dimenziós euklideszi térben, és hagyja # 61485; pont ebben a térben.
Vegyünk két pontot és. tartozó .Mnozhestvo pont. amely lehet leírni
(A koordinátákat van írva a következő:
,
Ez az úgynevezett konvex és kombinatsieytochek
szegmens. pontokat összekötő és. Rámutat magukat, és az úgynevezett a végén a szegmens. Azokban az esetekben, n = 2 és n = 3 # 61485; szegmens a szokásos értelemben vett a síkban, vagy a térben (lásd. ábra. 12). Megjegyezzük, hogy ha # 61548; = 0. és amikor # 61548; = 1. azaz a # 61548; = 0 és # 61548; = 1 megkapjuk a szegmens véget ér.
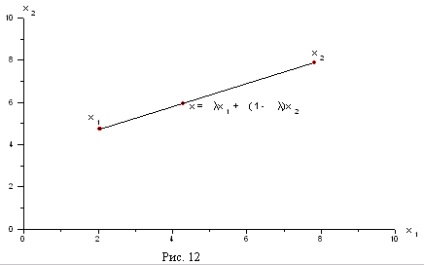
,
ahol minden nevezzük konvex kombinációja pont.
Legyen néhány régióban térben (más szóval,
G pontok halmaza
Definíció. A készlet (terület) konvex. ha az a tény, hogy az következik, hogy # 61548; # 61646; [0,1]. Más szóval, a G # 61485; konvex halmaz, ha igen, együtt annak két pontot tartalmaz, amely összekötő szakasz ezeket a pontokat.
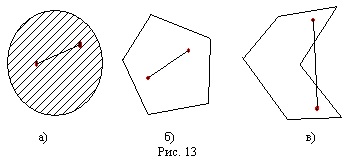
Ezeken az ábrákon „a” és „b” - konvex halmazok, és a „c” nem egy konvex halmaz, mert van egy ilyen pár pontot adott szegmens összekötő őket egyáltalán nem tartozik ebbe a körbe.
1. Tétel Legyen G # 61485; konvex beállítva. Ezután minden konvex kombinációja pontok tartozó ezt meg is tartozik ehhez a készülékhez.
# 61485; pont tartozó set G.
Belátjuk a tétel indukcióval. Ha k = 2, a tétel igaz, mert egyszerűen belép a meghatározása a konvex halmaz.
Tegyük fel, hogy a tétel igaz valamely k. Vegyük azt a pontot, és megvizsgálja a konvex kombinációja
,