A tulajdonságait binomiális együtthatók
A binomiális együtthatók értékei
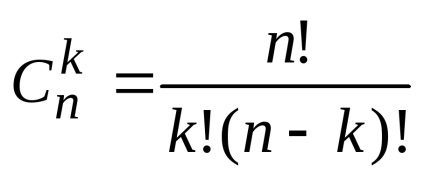
amelyek kifejezik a kombinációk száma az n elem szállító technológia. Ezeket az értékeket a következő tulajdonságokkal rendelkezik.
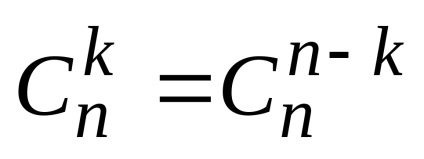
A képletben a binomiális, ez azt jelenti, hogy az együtthatókat, állva a ugyanabban a helyzetben a bal és jobb oldali végéhez a képletek, például:
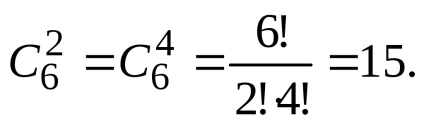
Tény, hogy
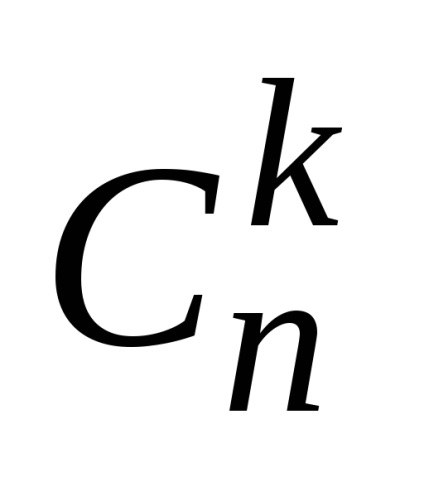
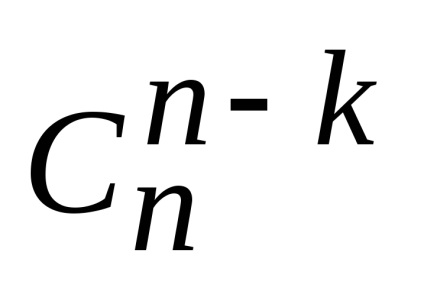
Let. szám
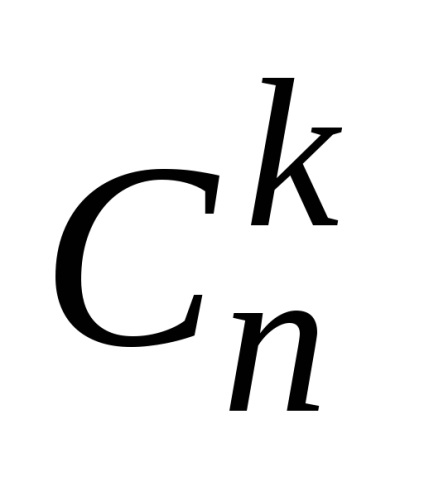
1) A részhalmazát nem tartalmazó elem
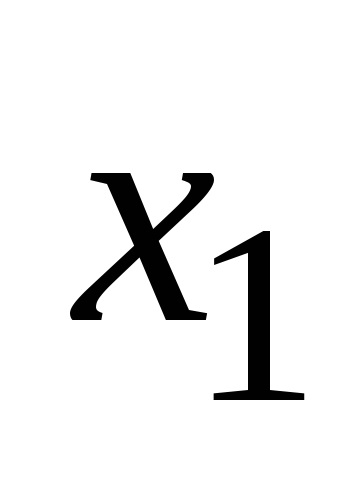
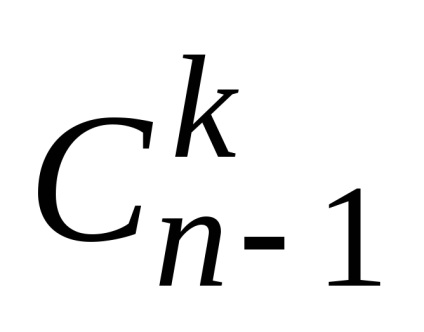
2) egy részhalmaza tartalmazó elem
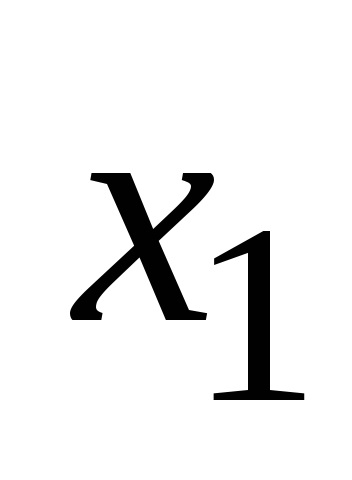
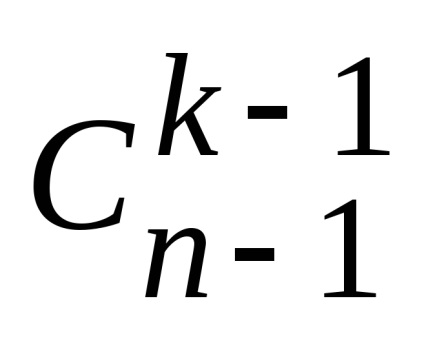
mert Ezek az osztályok nem metszi egymást, akkor a szabály összegzi a szám minden k elemű részhalmaza egyenlő mnozhestvaX
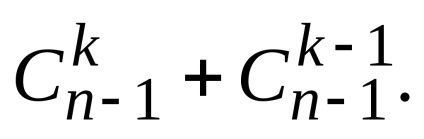
Ennek alapján az ingatlan az építési Pascal háromszöget (ábra. 2.2) az N-edik sorban, amelyek az együtthatók a binomiális bővítések
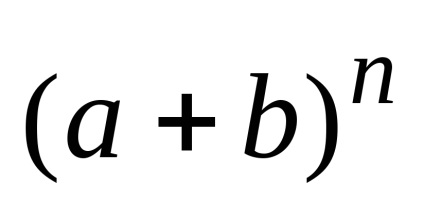
Behelyettesítve Eq binomiális
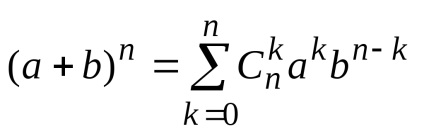
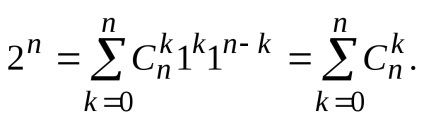
Megjegyezzük, hogy mind a halmazelmélet fejezi számának összege az összes podmnozhestvn -element készlet. Ereje által logikai tétel (ld. 1.4.4), a szám
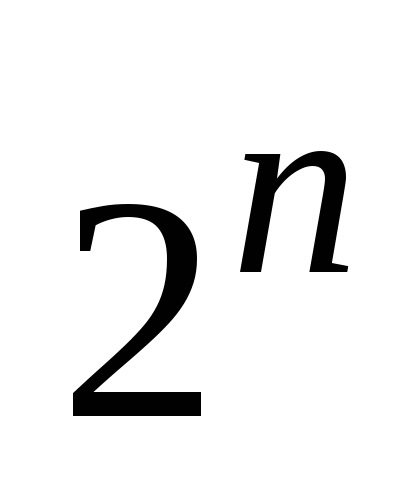
Állítsa be a binomiális tétel
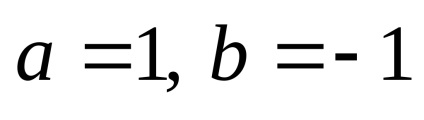
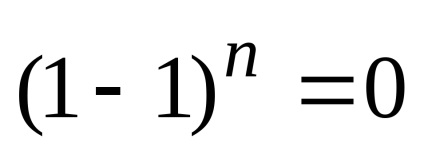
Az utóbbi tulajdonság kényelmes írni, mozgó minden együttható negatív jelek a bal oldali részén a képlet:
Ezután ingatlan könnyen tárolható a verbális készítmény „Összefoglalva binomiális együtthatók páratlan számok összegével egyenlő a binomiális együtthatók a páros számok.”
Feladat. Keressen egy tagja a binomiális expanzió
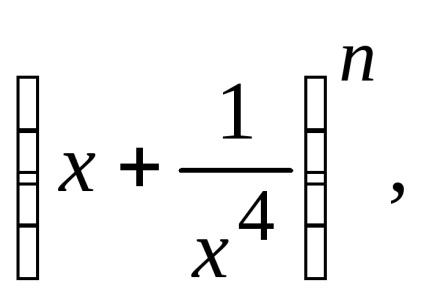
Határozat. Property által különbség összegét binomiális együtthatók páros számú is egyenlő 512, akkor az összeg az összes együttható egyenlő 512 + 512 = 1024. De az összeg a vagyon, ez a szám. ezért
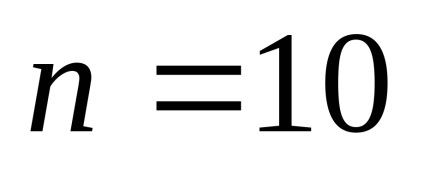
kifejezés az expanziós
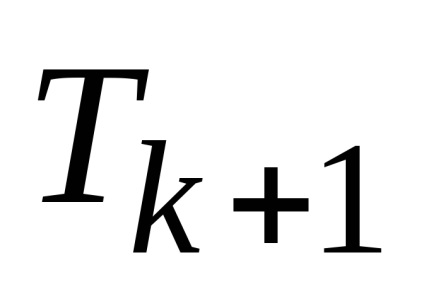

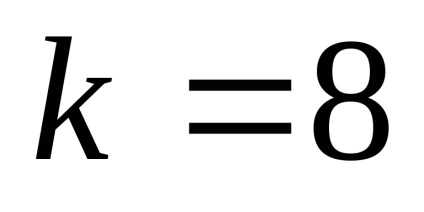
maximális tulajdon. Ha a mértéke binoman - még közül binomiális együtthatók a maximuma
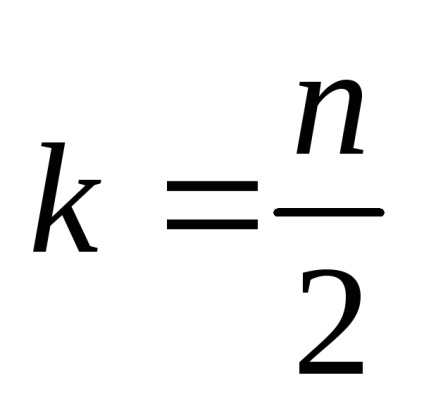
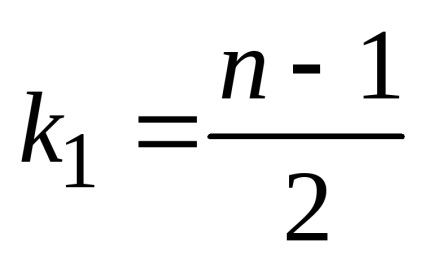
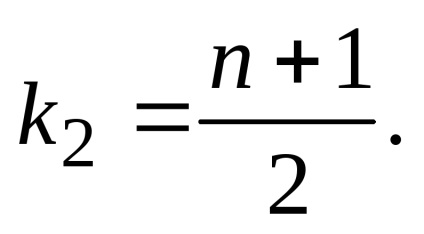
Így, amikor
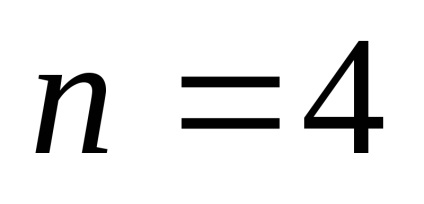
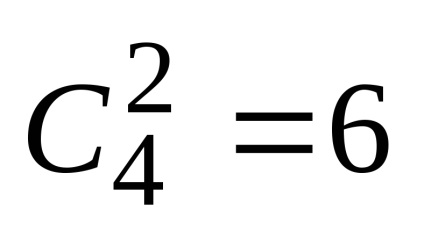
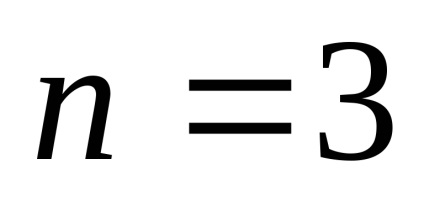
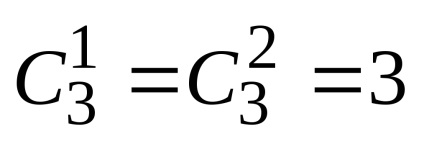
2.1.13. Hozzávetőleges számítás szerint a Newton binomiális
Állítsa be a binomiális tétel
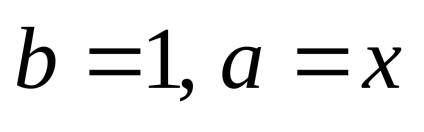
Ez a képlet kényelmes használni közelítő számítások a kis értékei esetén x (
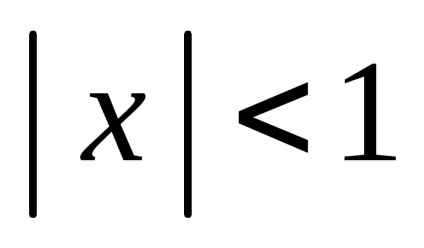
1. példa Newton binomiális képlet, Compute
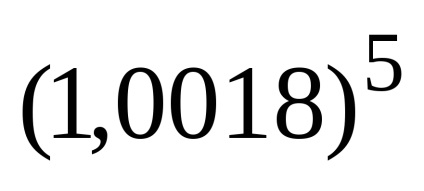
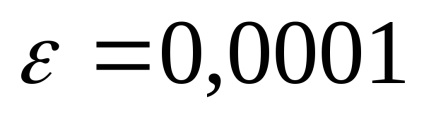
Szerint a fenti képlet, van:
Úgy becsüljük, a harmadik kifejezés ebben az összegben.
A többi feltétel kevesebb. Ezért az összes feltételt a harmadik lehet dobni. majd
Példa 2. Számítsuk
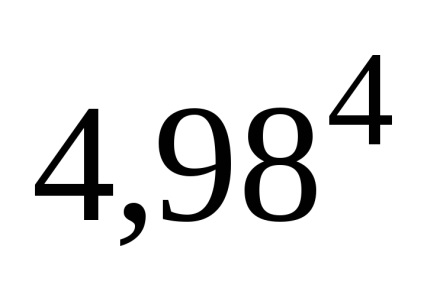
Úgy becsüljük, a harmadik ciklus:
.
Úgy becsüljük, a negyedik szám:
Tehát minden szempontból a negyedik, lehet dobni. megkapjuk