A transzformációs mátrix, webreference
A transzformációs mátrix kiszámítására használjuk az új koordinátákat az elem céljából a transzformáció, és lehetővé teszi, hogy telepíteni több transzformációk egyszerre. Különbséget tenni a két-dimenziós és háromdimenziós mátrixot, ezek eltérnek egymástól a méret és a tér, amelyen orientált. Mivel a kétdimenziós mátrix kisebbek, és ezért könnyebb vizsgálni az általános elvet, a mátrix példáját.
Kétdimenziós mátrix
Átalakítás egy kétdimenziós mátrix történik a képernyő síkjában, valamint az alábbi feltétel az, hogy a vonalak mindig párhuzamosak, így átalakítás megengedett forgatás, méretarány, döntés, és változtassa meg a helyzet, de nem a kilátás, vagy valami hasonló. Ez a munkaterület háromdimenziós mátrixban. Ábra. Az 1. ábra a megengedett átalakítások és lehetetlen készült kétdimenziós tömböket.
De ne így legyen
Ábra. 1. transzformálása elem
A mátrix maga a mérete 3x3, és általánosságban írhatjuk:
Az egyszerűség kedvéért néha a harmadik sorban csökken, mert nem befolyásolja a végeredményt. Az új koordinátáit minden egyes pontja az elem szorzataként kapott transzformációs mátrix mátrix koordinátákat.
És értékét a következő képlet szerint:
A szerepe az egyes együttható mátrix táblázatban látható. 1.
Táblázat. 1. transzformációs mátrix együtthatók
Megváltoztatása a vízszintes skála. Érték nagyobb, mint 1 elem nyúlik, kevesebb, mint 1, ellenkezőleg, zsugorodik.
Függőleges dőlés. A pozitív érték dőlést negatív le.
vízszintes dőlésszög. A pozitív érték ponyvák balra, jobbra negatív.
Megváltoztatása a függőleges skála. Érték nagyobb, mint 1 elem nyúlik, kevesebb, mint 1 - tömöríti.
Offset képpont vízszintesen. A pozitív érték eltolódik az elemet a jobb egy előre meghatározott számú képpont, a negatív érték balra tolódik.
Offset pixel függőlegesen. Amikor a pozitív elem csökken egy előre meghatározott számú pixel felfelé vagy lefelé egy negatív értéket.
mátrix () funkció használható a mátrix-transzformációval. együtthatók vannak felsorolva a zárójelen belül.
identitás mátrix
Ha mátrix együtthatók a és d értéke 1, és a maradék a mátrix elemei nulla, akkor ez a mátrix nevezzük egységet. Ez a mátrix az alapértelmezett, mert nem vezet semmiféle eleme az átalakulás. Tehát, ha kell, hogy csak az egyik fajta változás, az identitás mátrix kell alapul venni.
vízszintes Scale
Ahhoz, hogy fokozzuk a sejtek méretének, mondjuk, kétszer vízszintesen, egy együtthatót kell állítani 2, és a maradék együtthatókat elhagyni, mint egy egység mátrix.
Hiszünk az új koordináták:
x „= 2 * x + 0 * y + 0
y „= 0 * x + 1 * y + 0
skálázásához kódot 1. példában mutatjuk be.
1. példa méretezés
A példa eredményét az ábrán látható. 2. blokk szöveges 20% -kal megnyújtott vízszintes irányban.
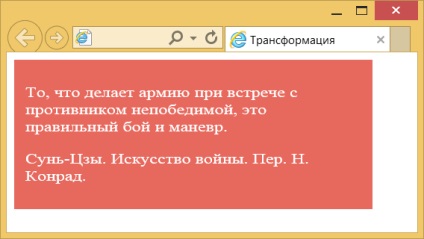
Ábra. 2. Állítsa be a szöveg méretét
A vízszintes reflexiós elem kell beállítani a = -1. Függőleges d = -1 vagy mindkét érték egyidejű egy időben, hogy az tükrözze vízszintesen és függőlegesen.
2. példa mutatja tükrözi a szöveg függőlegesen.
2. példa Reflection
A példa eredményét az ábrán látható. 3.
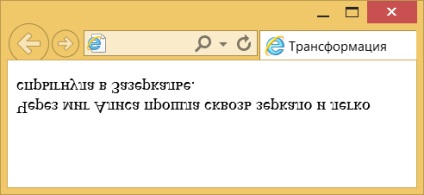
Ábra. 3. Reflection szöveget függőlegesen
Dönthető és reagálni együtthatók b és c. és amelyek befolyásolják az elem típusát. Állítsunk c = 1, és milyen átalakítások kapunk.
x „= 1 * x + 1 * y + 0
y „= 0 * x + 1 * y + 0
Így a változó csak a koordináta x. amely növekszik a y érték. ami a ponyva tagja. 3. példa használt egy negatív értéket a C faktor dönthető jobbra.
3. példa dönthető
A példa eredményét az ábrán látható. 4.
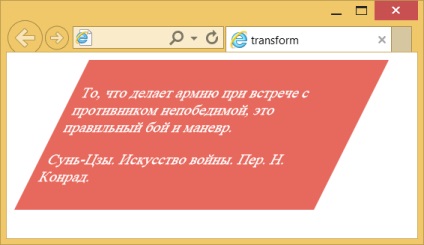
Ábra. 4. Tilt egység
Forgatás kombinációja skálázás és szurok, de tartani az eredeti arányokat átalakító elemet meg kell felelniük a szigorú számítás segítségével szinusz és koszinusz.
Self forgás az óramutató járásával megegyező, α meghatározza a forgásszög fokban.
elmozdulás
A vízszintes elmozdulás elem felelős tx együttható. és függőlegesen ty. Az érték szolgál a pixelek száma.
Háromdimenziós mátrix
A háromdimenziós mátrixot, amelynek mérete 4x4, és használják a koordináta konverziós elem háromdimenziós térben. Általánosságban elmondható, hogy ez így néz ki:
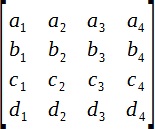
A név „háromdimenziós” csupán azt a tényt tükrözi, hogy a mátrix úgy tervezték, hogy a 3D-s térben. Kétdimenziós mátrix egy speciális eset és 4x4 mérete a következő:
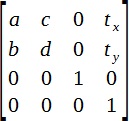
A tiszta formájában ez a mátrix ritkán használják komplexitásuk miatt, és jelenléte kényelmes funkciók transzformációra helyet. Ha érdekel a trigonometria és a koordináta-transzformáció képletek más, akkor olvassa el ezt az anyagot.