A tömegközéppont néhány számadat
Triangle. A tömegközéppont metszéspontjában annak mediánok. A geometria Ismeretes, hogy a a háromszög középvonalainak metszik egy ponton, és vannak osztva egy arány 1: 2 a bázis.
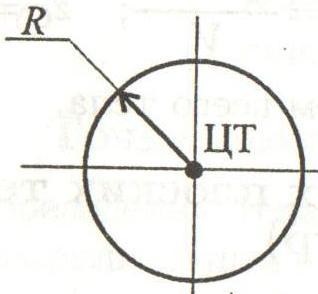
Kör. Mivel a kör két szimmetriatengely súlypontjának a kereszteződésekben a szimmetria tengely.
Félkör. Félkör van egy szimmetriatengelye, a súlypontja ezen a tengelyen. Egyéb koordinátája a súlypont képlettel számítottuk ki :.
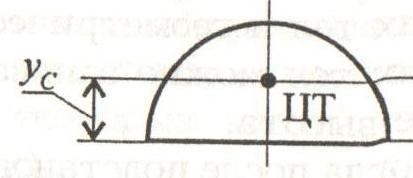
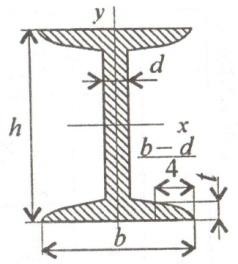
Sok alkatrészek, amelyek szabványos - az átütemezett, I-gerenda, csatornák és mások. Minden méretben, valamint a geometriai jellemzőit hengerelt szakaszok táblázatos adatok megtalálhatók a kézikönyvekben lévő táblázatokban normál nyomtávú (GOST 8239-89, GOST 8240-89).
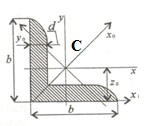
1. példa Annak meghatározására, a helyzetben a súlypont a szám az ábrán látható.
Mi választjuk ki a koordináta tengelyeket, hogy az x-tengely áthalad a legalsó méretek, és az y tengely - a bal dimenzióit.
Felosztása egy komplex szám a minimális számú egyszerű formák:
Számoljuk ki a terület minden egyes egyszerű forma, annak súlypontja koordináták. számítási eredményeket az A táblázatban