A töltés eloszlása a vezetékek
A töltés eloszlása a vezetékek.
Fémvezetékekhez általában semlegesek: mindkettő egyaránt negatív és pozitív töltések. A pozitív töltésű - ionok a kristályrácsban, negatív - mozgó elektronok szabadon a vezetőt. Amikor a vezető számolt be túlzott mennyiségű elektront, ez lesz a negatív töltésű, ha a vezető „kiválasztott” egy bizonyos számú elektronok, akkor pozitív töltésű.
Ennek hiányában a területen belül az üregbe vezető teremt elektrosztatikus védelmet. Vezeték vagy egy kellően vastag fém háló, a környező minden oldalról egy bizonyos régióban, árnyékolja, hogy az elektromos mezők által létrehozott külső ráfordítások.
Az elektrosztatika tekinthető egyenletes, állandó költség forgalmazás. Stacionaritást feltétel egyenlő nullával belül vezető mező E = 0. Ha a feszültség nem egyenlő nullával, akkor ez létre elektromos erők okozza irányított mozgását az elektronok, azaz az elektromos áram ...
Túlzott díjak jelentették vezető egyenletesen oszlik csak a felület felett a fém gömb vagy labdát. Minden más esetben, díjak egyenlőtlenül oszlik: minél nagyobb a görbülete, annál nagyobb a felületi töltés sűrűség a felszínen a karmester. Lássuk be ennek. Vegyünk két labda sugara R1 és R2. felszámított díjak Q1 és Q2. volt. Csatlakozz őket drót. A díjat a labda az egyik a másikra, amíg lehetséges az egész rendszer nem lesz ugyanaz. A hatása a huzal nem lehet figyelmen kívül hagyni.
a potenciálok a töltött gömbök, hogy azok a vegyületek
A töltés eloszlik a felület felett úgy, hogy a felületi sűrűség s értéke fordítottan arányos a görbületi sugár a felület
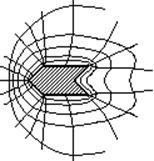
Mi található a térerősség töltésű vezető felszíne közelében. A Gauss-tétel. Felülvizsgálata vezeték képezi egy ekvipotenciális felületet. Távvezetékek merőlegesek az ekvipotenciális felületek. Mi választjuk ki a Gauss-felület S henger nagyon kis méretű, amelyek merőlegesek a formázó felület a vezeték (lásd. Ábra.). A hengeren belül felületi töltéssűrűség s feltételezzük, hogy állandó.
Azt ossza be áramlását három integráns: mellett az alsó végén, és felső vége felületek. Az első szerves = 0, a cosa = 0. második integrál = 0 és t = 0. Azt kapjuk E ....:
T. Hogy. Szürke háttér egyenlő a felső végén területe a térerősség közvetlenül a felületen arányos a felületi töltéssűrűség.