A tér az átfogója

Azt mondják, hogy a szakterületen a geometria építésére egy megfelelő igazolást a rossz rajzok.

Ezen ősi agyagtábla ábrázolja négyzetgyök kettő számított legfeljebb három karakter a hatvanas rendszert alkalmazták, a babiloniak, körülbelül ie 1700. Photo Bill Casselman

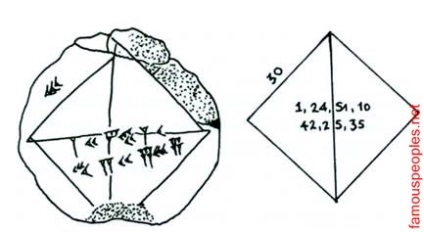
Babilóniai ékírásos számok az oldalán és átlók a tér (a bal oldalon) megfelelnek a modern (jobbra) egy szögletes oldalsó 30, amelynek kiszámítása átlós. Két írt számok (a hatvanas számítási rendszer), így: az első - 1,414212963, jó közelítéssel a négyzetgyök 2; második - 30 x 1,414212963 termék, átlós hossza, összhangban kiszámított a Pitagorasz-tétel

Euclid össze az ötleteket a nagy matematikusok a pythagoreusok, például Arkhütasz, valamint a munka Hippokratész Eudoxus és Theaitétosz, add saját gondolatai és kombinált logikai sorrendben az úgynevezett „Elements”. Ez a munka áll 13 rövid könyvet, ő lett a leghíresebb tankönyv az emberiség történetében. Ez egy nagy kincslelet finom matematikai érvekkel igazolja a hatalom a axiomatikus módszer akcióban. Euclid vette alapul a nettó axiómák, vagy küld, és rendszeresen használja logikai szabályok épült teorem28 bizonyítékokat. Ezt a technikát aprólékos levonás vált modell a tudósok különböző területein sok évezreden. Tól Fomy Akvinskogo a Spinoza látjuk módszerével érvelés, amely tükrözi a szerkezet Eukleidész bizonyítékokat. Fejlesztési filozófiai gondolkodás elválaszthatatlanul kapcsolódik a fogalom a filozófusok és teológusok a matematika, amit részének tekinthető abszolút dolgok lényegét, nem pedig csak egy leírást vagy modell a valóság.

Elejéig a XIX században úgy vélték, hogy az euklideszi geometria írja le a tényleges valós térben. Amikor Riemann, Lobacevskil, Bolyai és Gauss megfogalmazott azok nem-euklideszi geometria struktúráját leíró nemlineáris felületek, például gömb vagy nyereg összerázzuk filozófia a maghoz. Euklideszi geometria hirtelen lett csak egy a sok közül: teljes és logikailag konzisztens, mivel a saját meg a megdönthetetlen axiómák. Így, geometriai felfedezések hozzájárultak a relativisztikus gondolkodás. Abszolút igazság elutasították geometria, valamint a politika, a vallás és a kultúra.

Nincs vita, a szélessége és mélysége a hatást, amelyet elő a könyveket Euclid, példátlan. De van egy tárgyat, majd egy ismert kép a tanításait, amely ismertté vált, hogy az összes többi. Ez az utolsó a 48 tételek az első könyve a „Elements”: ingatlan, a minden derékszögű háromszögek és számunkra ismerős néven Pifagora29 tétel. Vegyünk minden derékszögű háromszög oldala A, B és C, ahol C - a leghosszabb oldala (átfogója), akkor A2 = B2 + C2.

Az egyik legenda szerint Püthagorasz (kb 580-500 BC) fedezte fel ennek a tételnek a palota Polycrates, a zsarnok uralkodó a szigeten Samos. Várakozás, amíg felvették az uralkodó, Pitagorasz tanulmányozta a mintát a padlón, a külső szobában a palota. Ez egy mozaik négyzetek. Észrevette, hogy ha húzol egy átlós vonal, amely elválasztja a tér két derékszögű háromszög, a terület a tér épül a diagonális lesz egyenlő a két négyzet a tér, beépített oldalán. Más szóval, a tér a átfogója egyenlő a négyzetének összege a másik két oldalán a háromszög. Ez egy olyan eset, ahol a fenti képletben A = B. Nos, egy érdekes történet!

Az „Elemek” euklideszi tétel azt mutatja, egy általános helyzetet, amikor egy nem feltétlenül egyenlő a B, hivatkozva a rajz, amely némileg hasonló vonalon köpenyt, amely egy esküvő bevont nevesty30 széket. A tétel kimondja, hogy a terület a négyzet egyenlő a területek összege BCED terek Hanks és GABF.

Tény, hogy több száz különböző igazolások a Pitagorasz-tétel, és tudjuk, hogy ez volt ismert az ókori babiloniak, kínai, indiai és egyiptomi hosszú születése előtt Püthagorasz. Babiloniak tudta, hogyan kell építeni egy háromszög A, B és C, megfelel az arány a Pythagoras, még mielőtt ie 1600.

Egy kis ékírásos táblák Photo kerül a fejezet elején mutat téren és átlós. Felírva ez a ék jelenti oldalainak hossza a vegyes tizedes hatvanas számolási rendszert alkalmazták, a babiloniak. oldalán a tér egyenlő 3 x 10 = 30; ismerve a Pitagorasz-tétel, ha feltételezzük, hogy a hossza a átló 30 x V2, azaz az arány a átlók egyenlő a négyzetgyöke 2. Itt, a hatvanas számrendszert (amelyben a szorzás 30, mint egy osztást 2), a hossza a diagonális nyilvántartani 42; 25,35 és 1; 24,51,10 egyenlő négyzetgyök 2. Ha az átadás a felvételi hatvanas decimális kiderül, hogy Babilon érték: 1 + 24/60 + (51/60 2) + ( 10/60 3) = 1,41421296, amely kiváló közelítés, a legpontosabb hat tizedesjegy pontossággal (négy és hatvanas számjegy).

A Pitagorasz-tétel egyik korai görög példányban a „Elements” Euclid

A legkorábbi ismert bizonyíték a Pitagorasz-tétel bizonyos értelemben egyedi és gyönyörű. Megtalálható a legrégebbi fennmaradt kínai matematikai értekezéseket - „Canon számítás Chou gnomon” egyes részei nyúlnak vissza mintegy 600 m-BC. Meg kell felhívni négy azonos derékszögű háromszög oldala A, B és C egy nagy tér. Ezután nyilvánvalóvá válik, hogy egy nagy terület a négyzet (A + B) 2 = A2 + B2 + 2AV összegével egyenlő területek négy háromszög, azaz 4 x 1 / 2AV plusz egy kis központi tér területén C2. Ebből következik, hogy A2 = B2 + C2. Vagy még egyszerűbb - mozgatni négy háromszög a nagy téren, így alkotnak egy-egy téglalap.

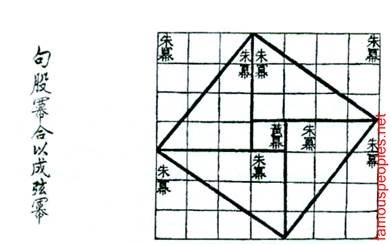
Kínai képe igazolást a tétel Pitagorasz ie 600: egy nagy terület a négyzet egyenlő a területének összege négy derékszögű háromszöget és egy kis négyzet belsejében

Látni fogja, hogy a területen belül a tér, nem terjed ki a háromszög mindkét képen ugyanaz lesz, így A2 + B2 - C2.

Hozzátehetjük, hogy rosszul rajzolta rajzok forrása lehet a súlyos hibákat. A középkorban volt a koncepció falsigrafiya, mely rossz rajzait és bizonyítékokat. A munkaigényes folyamatot a másolás ősi kéziratok kézzel gyakran vezetett arra a tényre, hogy az ábra eltelt vagy másolt inkább hanyagul. Ugyanezen okok miatt néha bizonyulhat telt el, és csak a kiválasztott rajzok szemléltetésére bocsátjuk megoldások tétel. Arra is van példa, ahol a számok vannak, de nem kíséri magyarázatokat, hogy a könyv a problémákat, hogy tudunk kérdéseket kell megválaszolni. Lehet, hogy ez olyasmi, mint egy bölcsőt, mint azok használják, hogy felkészüljenek a vizsgákra? Vagy didaktikai anyagok rések kellett kitölteni a középkori diákok?

Ábrán és az ebben a fejezetben - nem egyszerűen tükrözi a hosszú története a híres tétele. Ezek és sok hozzájuk hasonló, már a parázs viták tárgyát képezte. 1934-ben, egy kis cég a francia matematikus, akinek a lelke volt André Weil, gyűjtenek egy kávézóban „Kapulad” a Latin negyed Párizsban. Elindultak fogalmazni a különböző ágak matematika az új szigorú formáját megvalósító belső mindet logikai szerkezetét.

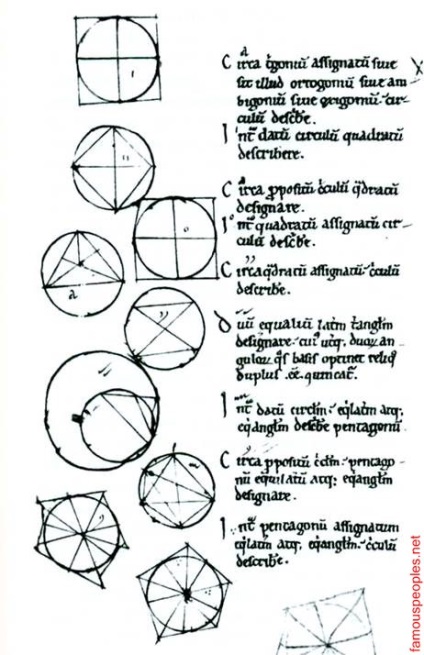
A negyedik könyve Euclid, egy kézzel írt példánya a XII században latinul. Itt állítják tételek bizonyítás nélkül és hiányos rajzok, hogy a diákok használhatják megbélyegzi és befejezni a bizonyíték. Eredeti összeállított Adélard Bath, amelyben a másolat készül, nem tartalmaz bizonyítékokat. Vegyük észre, hogy minden kép tartalmaz megjegyzéseket vagy jelek, amelyek jelzik, hogy az olvasó, amelyre az vonatkozik nyilatkozatot. Például egy nagy kört egy kis kör belsejében (negyedik alulról) van jelölve két kullancs, amely összeköti azt a jóváhagyást a hatodik a listán, amely betűvel jelölt d

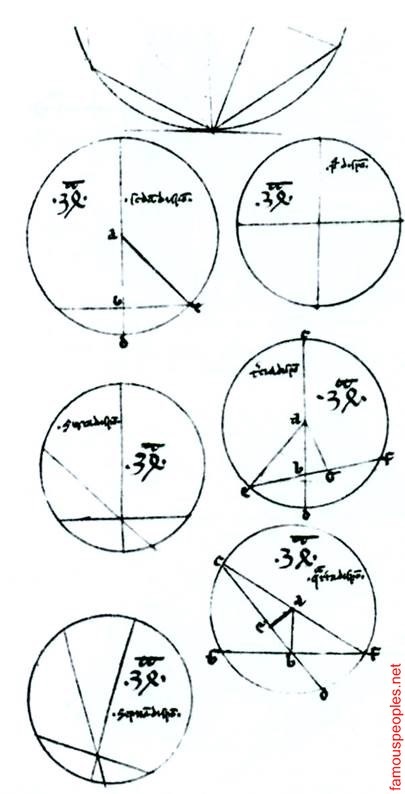
A töredék egy kézirat a XIV században, ahol az elmulasztott nyilatkozatok és igazolások Euklidész tételeit, de megmentette a mellékelt ábrák, hogy az olvasók is felér bizonyítéka saját. Ez azt mutatja, különböző esetekben Tétel 3.4 Book III, amely megállapítja, hogy bármely akkord metsző kör szegmensek egyik akkordok egy téglalap, amelynek területe egyenlő a téglalap területe által meghatározott szegmensek a második akkord. A különböző ábrák különböző esetekben a elrendezése akkordok

Először knizhka- „kagyló” elkötelezett a háromdimenziós geometria. Az első fordítása Euclid angolra, megjelent Londonban 1570-ben a cím alatt „Elements of geometria, az ókori filozófus Euclid Megara, mint (az első alkalommal) lefordították angol Henry Billingsleem” ügyesen használjuk térfogati kibontakozó illusztráció.

Bourbaki szövegek a kör tagjai voltak során kialakult vita és kíméletlen kritika. Először jelent meg a különböző fragmentumokat a modern matematikai jelölések és terminológia, és most nagyon kevesen tudják, hogy mi a létét Bourbaki. Azonban a munka Bourbaki tette a hatását, hogy sok matematikus, különösen az alkalmazás, úgy romboló. Támaszkodott a matematikai struktúrát kárára problémák és példák. Nem volt rajzokat. Matematikai intuíció volt, úgy tűnt, zárt kényszerzubbonyt axiomatikus. A hangsúly a közös struktúrákat különböző matematikai kutatás végül lett befolyásolja az iskolai tananyag számos országban, aminek következtében az úgynevezett új matematikafilozófiát. Fejlemények azt mutatják, hogy ez a technika sikertelen volt. Elmagyarázta nehéz fogalmakat túl korán, ráadásul anélkül, hogy oldja meg a problémákat, az iskolában a gyerekek nehéz volt fejleszteni matematikai készségek és hozza létre a szükséges motivációt. Ugyanilyen fontos, hogy az új módszer nem teszi lehetővé a szülők, hogy segítse a gyermekek számára, mert egyszerűen nem volt tisztában az „új matematika”.

Bourbaki csoport akarták kitörölni a gyakorlatban a bizonyítékok a rajz, ahol a fő szerepet játszott a matematikai érvelés rendszerben.

Ez a filozófia nem volt teljesen új. A jól ismert négy térfogat „Analitikai Mechanics” Lagrange (1788) azzal jellemezve, hogy teljes hiánya geometriai rajzok és ötletek.

Nagy Lagrange elődje, Isaac Newton használta a rajzokon, ahol hasznosak voltak, mint mi most. Hiszen tudjuk, hogy ha lehetséges bizonyíték a rajz, van egy módja annak, hogy megfogalmazzuk és logika és alkalmazza a megoldást számos példát nem feltétlenül terjed ki a minta nem mindig egyértelmű az ilyen lelki szemei ​​előtt. Euclid például igyekeztek összefoglalni az eredeti Pitagorasz-tétel helyett a terek, a másik oldalán egy derékszögű háromszög alakú.

1980 után alapvető kör tagjai Bourbaki nyugdíjas, és véget ért a lomha pert kiadók, ez csökkent. Több mint 20 év telt el anélkül, hogy említésre méltó kiadványok válogatott, és az ő befolyása meggyengült. Talán egyszerűen túl szerelmes kép? De ez a következtetés talán túl könnyű laknak rajta. Bourbaki és elutasítja sok matematikus azt mutatták, hogy a matek nem két kultúrában. Ők azok, akik inkább építeni a struktúrát és hivatalossá nagyfokú általánosság és azoknak, akik szeretik a póz és konkrét problémák megoldásához (bár nem matematikus nem tulajdonítható kizárólag az egyik ilyen táborok). Ez néha uralja az absztrakt módszereket, és fordítva. Ez a különbség a vélemény, hogy melyik a tendenciák (vagy kellene) az uralkodó, talán, lehet tekinteni egy jó jel, azt mutatja, hogy még mindig van egy egészséges egyensúlyt a kettő között.

Kapcsolódó hozzászólások:

«Előző csillag csillagos éjszaka. Whirlpool Galaxy Next „Világok harca. Mars-csatorna