A téma az áramlás vektor egy zárt Gauss ma - Vector Field Gentz - studopediya
§1. Áramlási vektor a zárt felület. Tétel Gauss.
4.1 Tétel Ha egy bizonyos régióban a tér vektor koordináták G
folyamatos és folyamatos származékok. az áramlási vektor bármilyen zárt szakaszonként sima felület σ, területén elrendezett G, egy hármas integrálját V régió, által határolt felület σ:
(Gauss-féle formula) .Normal külső felületére σ vesszük.
Példa 4.1. Számítsuk ki a fluxus-vektor
egy zárt felület
x 2 + y 2 + z 2 = R 2 z = 0 (z> 0).
Határozat. Általános képlet szerint 4.1
A beépített (4.2) kényelmesen kiszámítani gömbi koordináták. van
volumentényezőt, és
Példa 4.2. Számítsuk ki a vektor áramlás az egész felületén a tórusz.
Határozat. A Gauss-tétel, azt kapjuk, hogy a kívánt áramlási P
ahol V - térfogata a tórusz. Térfogatának kiszámításához V. használata Tétel Gulden térfogata a forgástest, amelynek értelmében a az a térfogat megegyezik a termék a négyzet alakú darabot a forgó utat által leírt tömegközéppontja az ábrán forgás közben.
Tegyük fel, R1 és R2 jelentése - belső és külső sugara a tórusz (Fig.4.1). Area S kört képező forgása közben a tórusz, a
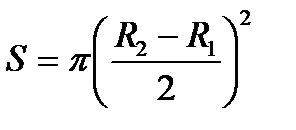
A hossza által leírt a tömegközéppontja - a központ ezt a kört, - az L hosszúság a kör sugara. azaz.
Így a V térfogata megegyezik a tórusz
Z n ° σ1 k j Y i σ2 X n ° = -k 4.2 ábra
Példa 4.3. A Gauss-tétel - Ostrogradskii kiszámíthatja az áramlási mező vektor
keresztül a külső oldalfelülete részét z = 1 - x 2 - y 2. felett helyezkedik el a gépet XOY.
Határozat. Annak érdekében, hogy képes legyen alkalmazni a Gauss-tétel - Ostrogradskii, csukja be az alsó felülete ez a darab XOY sík, ami csak egy kört
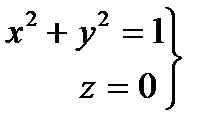
Legyen v - térfogata a kapott szilárd által határolt szakaszonként sima zárt felület σ. amely egy részét egy paraboloid forgástest σ1 z = 1 - x 2 - y 2 és részben σ2 sík z = 0. (4.2 ábra.).
Az áramlási egész felületén a vektor σ a Gauss-tétel - jelentése Ostrogradskii
Azáltal osziatószer lesz
Ennélfogva, a kívánt áramlási
És P2 áramlási irányt a kör
Mivel a sík z = 0, van
2. §. A divergencia a vektor mező.
A koncepció a fluxus vektor keresztül zárt felület vezet fogalmának divergencia vagy mező divergencia. Ez a koncepció ad némi mennyiségi jellemző a mező minden pontján.
Legyen M - vizsgált területen pont. Σ körülveszik a felület tetszőleges alakú, például gömb, kellően kis sugarú. Által határolt területen σ felületi. legyen (V), térfogata V. Tekintsük a hozzáállás
Meghatározás 4.1. Ha az arány (4,3) van egy véges határérték, amikor a terület (V) szerződött az M pont, akkor ezt a határértéket az úgynevezett vektor mező divergencia (divergencia vektor a) az M pont, és jelöljük div egy (M). azért, hogy
Általános képletű (4,4) ad invariáns meghatározását divergencia. Ez a meghatározás azt jelenti, hogy az eltérés a területen, és azon a ponton, M jelentése a térfogatsűrűség és a fluxus vektor ezen a ponton.
Pontok M és vektor mezőben (M), amelyben osztásnál a> 0. nevezett források, valamint a pont, ahol a div a<0 называются стоками векторного поля.
A divergencia vektormez® skalár függvény a területen pont.
Ha a koordinátákat a vektor
folyamatosan a részleges származékok közelében az M pont (x, y, z). Ezután a invariáns meghatározása divergencia tétel Gauss - Ostrogradskii kap, hogy a
Minden érték egyenlet (4,5) tartják ugyanazon a ponton M (x, y, z).
Használata képletű (4.5) a divergencia Gauss-tétel - Ostrogradskii (lásd §1.) Írandó vektor formában,
Példa 4.4. Használata invariáns meghatározott kiszámítja az eltérés a vektor egy = xi pontban O (0, 0, 0), kiválasztunk σ körülvevő felületek pont O. σε sugarú gömb ε középpontja ezen a ponton.
Határozat. A definíció szerint a divergencia ezen a ponton van
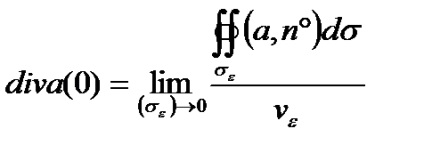
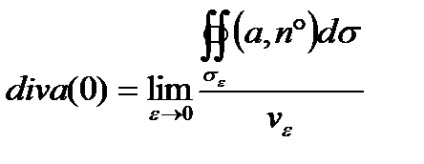
De ahogy a kötet egy gömb egyenlő az
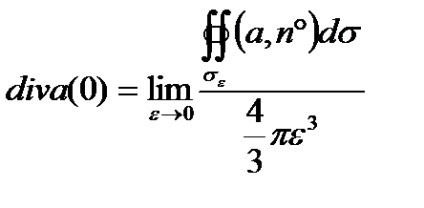
Kiszámítjuk a fluxust a gömb ezen vektor σε. A készülék normál vektor a mező n ° σε célzó gömb sugara, így nem tud:
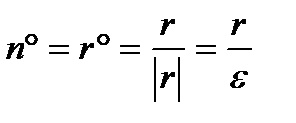
Keresek fluxus egyenlő
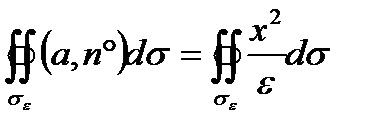
Rátérve a koordinátákat a gömbön σε
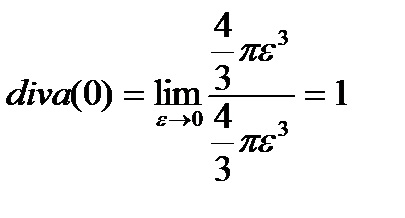
Példa 4.5. Számolja div r.
Határozat. Van = xi + yj + zk, úgy, hogy a P = X, Q = y, R = Z, és így az (4.5)
4.6 példa. Számítsuk div (u, a), ahol u (M) - skalárfüggvény, és (M) = P (x, y, z) i + q (x, y, z) j + R (x, y, z) k - vektor funkció.
Határozat. Képlet segítségével (4.5), azt látjuk,
Példa 4.7. Keresse meg a divergencia a vektor
ahol - a távolság a származási a változó pont M (x, y, z).
Határozat. Használata képletű (4,7), megkapjuk
.