A Riemann-sejtés
hipotézis
Birch - Swinnerton-Dyer
Bár nem találtam olyan mintát, amely leírja az elosztó prímszámok között természetes, Riemann találtuk, hogy a szám prímszám. nem haladja meg a x, - prime-számláló funkcióval. jelöljük # X03C0; (X) - kifejezve eloszlása úgynevezett „triviális nulla” zéta-függvény.
Sok az állítások a prímszámok eloszlása, beleértve a számítási komplexitás bizonyos egész algoritmusok. bizonyult a feltételezés hűség a Riemann-sejtés.
kiszerelés
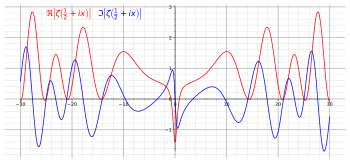
A tényleges (piros) és képzetes (kék) összetevőit a zéta-függvény
A függvényegyenlet # X03B6; (S) = s 2 # X03C0; s sin # X2061; # X03C0; s január 2 sin # X2061; # X03C0; s # X0393; (S) # X03B6; (1 # X2212; s) \ pi ^ \ sin> \ zéta (1-s)> 1, és le az explicit # X03B6; (S) = # X2211; n = 1 # X221E; # X03BC; (N) N s> = \ sum _ ^ >>> ha Re s> 1 \, s> 1>. ahol # X03BC; (N) - Möbius-függvény. ebből következik, hogy az összes többi nullák, az úgynevezett „nem-triviális”, található a szalag 0 # X2A7D; Re s # X2A7D; 1 \, s \ leqslant 1> szimmetrikusan az úgynevezett „kritikus vonal» 1 2 + i t. t # X2208; R + meg, \; t \ in \ mathbb>.
A Riemann-sejtés
Riemann hipotézis azt állítja, hogy:
„Az összes nem triviális nullákat a zéta-függvény valós része megegyezik 1 2 >>”
azaz, komplex számok találhatók a vonalon Re s = 1 2 >>.
Általános Riemann-sejtés
Általánosított Riemann hipotézis (Eng. Generalized Riemann hipotézis) az ugyanazon állítás általánosításhoz a zéta-funkciók, az úgynevezett Dirichlet L-függvények.