A problémák megoldását a differenciálegyenletek és sorozatok
4. A probléma megoldása
4.1. A differenciálegyenlet elsőrendű
elkülöníthető változók
1. példa Hayti általános egyenlet megoldása y ¢ cosx - (y + 1) sinx = 0.
Határozat. Szét a változókat. Ehhez megszorozzuk mindkét oldalról a szorzó helyett y ¢ Az egyenlet:
Mi integrálja az egyenletből Terminusonként kapjuk:
,
Kaptunk egy általános integrál egyenlet.
2. példa Keresse meg az adott egyenlet megoldása: ha y = 3, ha X = 1.
Határozat. Át az egyenletet formájában: 2ydy = (1 - 3x 2) dx. helyett y ¢
Integrálása mindkét oldalán az egyenlet, megkapjuk:
- általános integrál egyenlet. Behelyettesítve a kezdeti feltételeket y = 3 x = 1, megkapjuk:
9 = 1 - 1 + c. ebből következik, hogy a C = 9. A szükséges különösen oldat formájában:
4.2. Homogén differenciálegyenletek
elsőrendű
Példa. Integrálása egyenlet: 2x 2 dy = (x 2 + y 2) dx.
Határozat. Osztása mindkét oldalon 2 x dx. megkapjuk az egyenlet jobb oldalán, amely függvénye a kapcsolatot:
Tedd azt, akkor y = ux. Megkülönböztetünk szerezni egy egyenletet több változó:
.
Elválasztása után változók megkapjuk az egyenletet, elválasztott változók:
.
Integrálja helyettesítő, megkapjuk:
Megjegyzés. Az elválasztás változók osztunk x és (u - 1) 2 ami csak akkor lehetséges, ha x ¹ 0 és u ¹ 1. Az azonnali vizsgálat könnyen belátható, hogy az x = 0 és u = 1, azaz y = x ... Ők is megoldást az egyenlet, de ezek nem szerepelnek az általános integrál. Ilyen megoldások úgynevezett különleges.
4.3. Lineáris differenciálegyenletek
elsőrendű
1. példa Find általános egyenlet megoldása :.
Határozat. Osszuk mindkét oldalán az egyenlet által (1 + x 2), kapjuk:
- lineáris egyenlet. Mi megoldani azt a helyettesítési módszer y = u × v. majd helyettesíteni az értéke y és y ¢ ebben az egyenletben:
,
Válasszon egy függvény v, hogy az expressziós zárójelben egyenlő nullával:
.
Ezután (4.1) felírható egyenletrendszert:
Találunk egy függvény v az első egyenletből:
,
.
Integrálása, megkapjuk, hagyjuk c1 = 1, v = 1 + x 2.
Mi helyettesíti v értéke a második egyenletben a (4.2):
Point of U és V jelentése szubsztituált a y = u × v. kapjuk:
- az általános megoldás ennek az egyenletnek.
Tekintsük a probléma, ami egy differenciálegyenlet.
2. példa keresése görbét ponton áthaladó M0 (1, 4), és rendelkeznek azzal a tulajdonsággal, hogy minden szegmense a tangens, benne a koordinátatengelyek, oszlik felét az érintési pont.
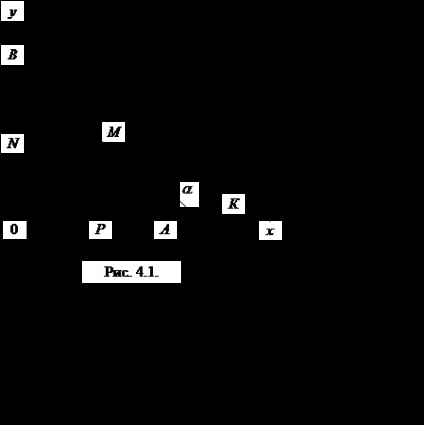
Határozat. Azt, hogy a rajz (ábra. 4.1). Legyen M (x, y) - tetszőleges pontja a kívánt görbe, AB - szegmens érintő a görbe ezen a ponton tartalmazott közötti koordinátatengelyek. By hipotézis, BM = MA feladat. Ha az OP - az abszcissza az M pontban DAMP
.
Azonban, PA = OP. ezért, hogy OA = 2x. OB = 2y.
Másrészt, mivel a
.
Következésképpen - differenciálegyenlet elkülöníthető változókat. Osztjuk a változókat, amelyek integrálják:
, .
Mivel a görbe át kell haladnia a ponton a M0 (1, 4), majd a helyett a koordinátái ebben az egyenletben, kapjuk: 1 × 4 = c. c = 4. Tehát a kívánt görbe egyenlet által definiált.
3. példa Tengeri hátráltatja mozgását hatása alatt vízállóság, amely arányos a hajó sebességét. Kiindulási hajó sebessége 1,5 m / s és 4 a sebessége 1 m / s. Keresse motorcsónak 12 másodperc után az elején a mozgás.
Határozat. Szerint a második törvénye dinamikájának differenciálegyenlet a mozgás a következő:
Ez differenciálegyenlet elkülöníthető változókat. Elválasztó változók, megkapjuk:
,
Behelyettesítve a kezdeti feltételek, azt találjuk:
Következésképpen ,. Az érték k / m jelentése helyettesítve a második kezdeti feltételeket: t = 4, v = 1 ,. Ebből következik: Tehát van egy adott egyenlet megoldása:
.
Helyettesítő Ebben az egyenletben t = 12, végül kapjuk:
.
4.4. Differenciálegyenletek, magasabb rendű,
így csökken a rend
1. példa integrálása egyenlet.
Határozat. Integrálása az egyenletben kétszer egymás után:
2. példa Find általános egyenlet megoldása:
Határozat. Ez az egyenlet nem tartalmazza kifejezetten a kívánt funkciót y. Elhelyezés egyenlet y ¢ = z. y ² = z ¢, megkapjuk lineáris elsőrendű egyenletet Z tekintetében (x) :. Cseréje z = uv, z ¢ = u ¢ v + uv ¢, megkapjuk:
Ez az egyenlet váltja az egyenletrendszert:
.
Oldjuk meg az első egyenletet:
Mi integrálja: c0 = 0, vagy helyettesítse a mért érték a v a második egyenlet :. Osszuk integrálni változó: ezért Visszatérve az eredeti változó y. kapjuk:
.
Osztjuk a változókat, amelyek integrálják:
az általános megoldás ennek az egyenletnek:
Példa 3. Keresse meg az általános egyenlet megoldása:
Határozat. Ez a differenciálegyenlet tartalmaz kifejezetten nem független x változó. Legyen y ¢ = p. y ² = p (dp / dy), behelyettesítve ez az egyenlet:
Mi választja el a változók vagy integrálni:
, .
Mivel p = y ¢, megkapjuk y ¢ = c1 (3 + y) - elsőrendű egyenletet elkülöníthető változók. Osztjuk őket: integrálni:
, , .
Egy általános megoldás ennek az egyenletnek.
4.5. Lineáris differenciálegyenletek
másodrendű
állandó együtthatós
Ahhoz, hogy megtalálja egy adott megoldást inhomogén lineáris egyenletek módszerével meghatározatlan együtthatók. A partikuláris megoldása az inhomogén lineáris egyenlet jobb oldalán egy speciális fajtája megtalálható utalva a jobb oldalon. Írva a táblázat a leggyakoribb esetben (4.1 táblázat.).
A jobb oldalon a differenciálegyenlet
A gyökerek a jellemző
egyenlet