A probléma egy paramétere, a modulrendszer
Problémák a - néhány igen nehéz a vizsga, de a legérdekesebb és. Megoldani őket - öröm. Azt javasoljuk, barátok, hogy a paramétereket, és nem kell félni a kihívásokat.
Feladat. Hogy milyen paraméter értékét, a rendszer több mint két megoldás?
Nyissuk ki a modult. Ő lesz lövés egy pozitív jel, ha podmodulnoe kifejezés nem negatív és negatív, ha podmodulnoe kifejezés kevesebb, mint 0:
Így kiválasztja a tökéletes négyzet, kaptunk két kört (vagy inkább azok részeire). Az egyik kört a vonal fölé van. és a második - az alábbiakban. Része a körök csatlakozott koordináták O (0, 0) és a C (-2; -4) - ez könnyen ellenőrizhető szubsztitúcióval.
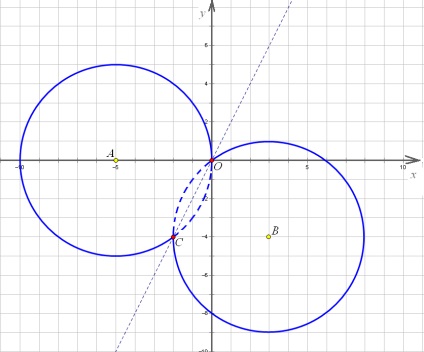
Kör metszi az egyenes meredeksége, amely állandó és az együttható - megváltozott:
Egy ilyen sor fog csúszni tengelyirányban felfelé és lefelé, mi érdekli az esetekben, ahol ez a sor több mint két metszéspont a „nyolc” a köröket. Kezdjük egy tanulmány a helyzet a vonal, amikor áthalad az origón.
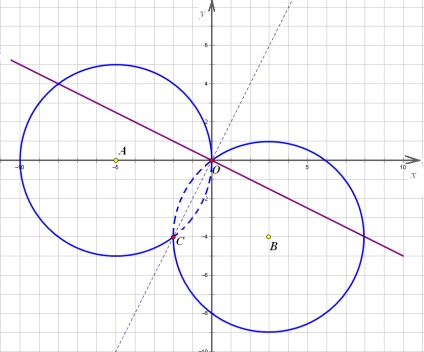
Ez egy extrém pont, amelynél a rendszer három megoldásokat. Alacsonyabb pozícióban a sor, hogy lesz egy ideig csak kétszer átkelni egy kört (addig, amíg eléri a C pont). De a nyírási egyenesen a származási látja, hogy a csomópontok a négy - és ez így lesz, amíg a vonal nem lesz kör érintője. Mi határozza meg a paraméter értékét, ha a származási egyenes. egyszerűen csak az esetben kiindulási pont koordinátáit O az egyenletben:
Most megváltoztassák a egyenesen, amíg meg nem érinti a kört. Ha a helyzet a vonal lesz képes meghatározni az egy pont koordinátáit, vagy pont - a trükk történik.
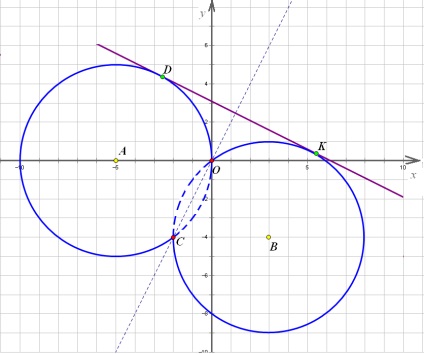
Gondolj bele: ha a sor, amelyet a körnek a sugara, felhívjuk az érintkezési pont azt kell perpedikulyaren. Figyeljük meg, hogy egyenes. lehatároló régió létezését körök meredeksége 2, és a vonal - lejtőn. és a terméket a két együtthatók (-1), úgy, hogy a közvetlen merőleges. Így beláttuk, hogy a vonal és a vonal, amelyik a sugár. ugyanolyan együtthatója hajlam egyenlő 2, azaz egymással párhuzamosan. Annak ismeretében, hogy a vonal, amely a sugár. Ez áthalad a ponton. Találunk az egyenlete.
A pontok közötti távolság, és az ismert - ez egyenlő a kör sugarát, amelyhez tartoznak ugyanazon a vonalon, a koordinátái ismertek - nem kerül semmibe, hogy megtalálják a koordinátákat.
Nézzük megoldani az első másodfokú egyenlet a rendszer:
Két gyökerei - a pontok koordinátáinak a tengely és az ellentétes irányú - mi szükség lesz rá, és mi jön vissza rá.
Most keresek egy paraméter, behelyettesítve a pont koordinátáit a egyenes egyenlete:
Nekünk egy kis győzelem: találtunk egy paraméter tekintetében, amelyek megfelelnek minket:
Zero belép ebbe a tartományba, mert három kereszteződések, de a második határ - nem megy le, csak két érintkezési pont és a szükség.
Kezdve a második távolságmérés:
Hasonlóképpen, egyszerűen helyett az egyenlet a pont koordinátáit, mi határozza meg a paraméter értékét abban az esetben, ha a közvetlen áthaladnak ezen a ponton:
Itt most az, amit kap vissza a második megoldás a másodfokú egyenlet: ez - a koordináta tengely pontot. .
Aztán koordináta az Y tengely:
Mi határozza meg a paraméter értékét:
Aztán a második intervallum a paraméter értékek :.