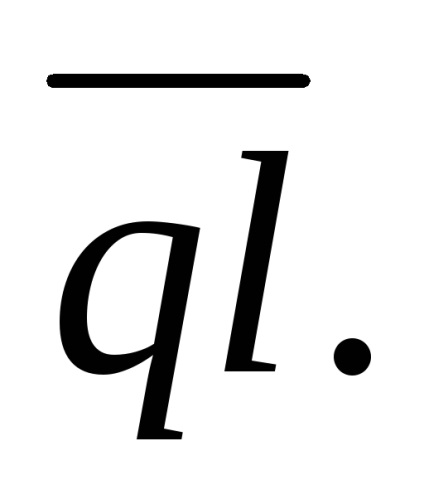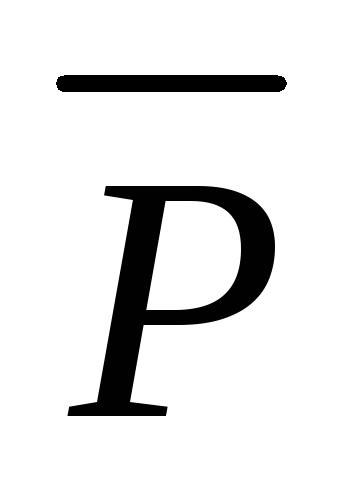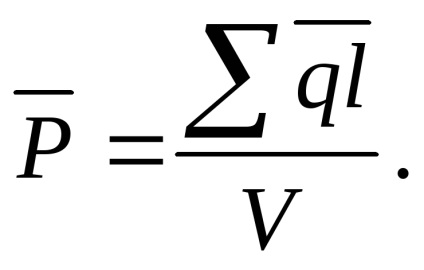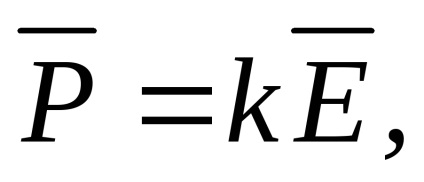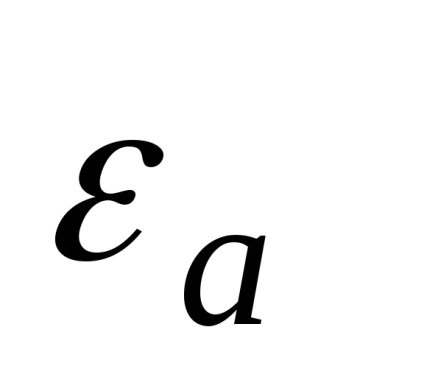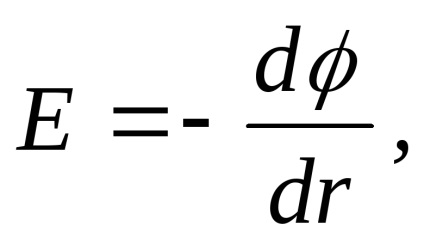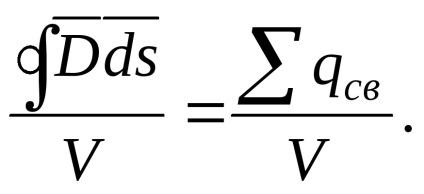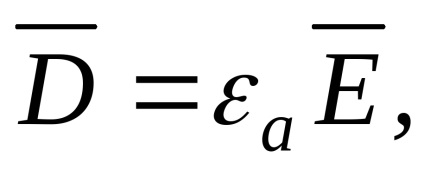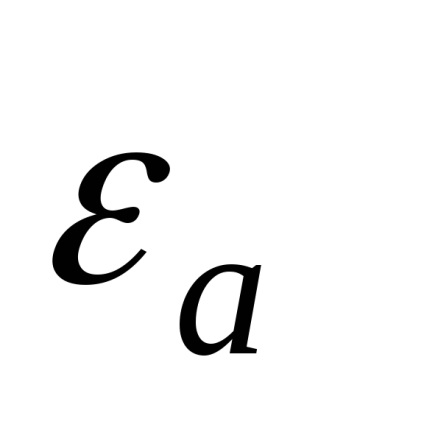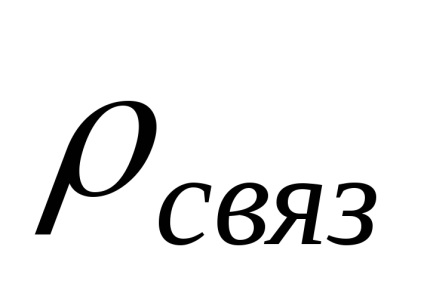Az anyagok megkülönböztetésére szabad és kötött díjakat. Szabadidő azok terheket, amelyek hatására az erőtér szabadon mozoghat az anyagban, a mozgás nincs korlátozva intramolekuláris erők. Kevesebb kötött díjak észre, hogy csak a molekulán belül eltolható hatása alatt a térerőt. Kapcsolódó díjakat nem lehet elválasztani az anyag így az összeg pozitív kötött díjak összege negatív.
Dielektromos testeket polarizált elektrosztatikus térben. Polarizációs érti a szabályos változása hellyel kapcsolatos díjak terén erők. Szemléletesen ki lehet mutatni, polarizációs ris.11.5, amely bemutatja a test hiányában az elektrosztatikus mező, és ha rendelkezésre áll. Ha a mező nincs jelen, akkor a molekulák (dipólusok) található a kaotikus rendellenesség (ris.11.5 is). Ugyanabban a testben a pozitívan polarizált kapcsolódó díjak tolódnak felé nagy potenciállal, és negatív - abba az irányba, a kisebb (ris.11.5, b), ahol az eltolt úgy, hogy az erőt a elektromos mező egyensúlyban intramolekuláris erők. Ennek eredményeként, a polarizáció a kitett felületen anyagok pozitív vagy negatív töltést kapcsolatos összege az első közülük pontosan megegyezik a második összeget. Dipólusokból létrehozhatják saját területén. A polarizált számít a kumulatív hatás nulla, és a polarizált - nem, ez vezet a gyengülését a kapott területén, és meg kell venni. Erre a célra, akkor a koncepció az elektromos dipólmomentum. Két elektromos pillanatban egyenlő nagyságú és ellenkező előjellel a díjak tartott szét rasstoyaniil. Ez a termék
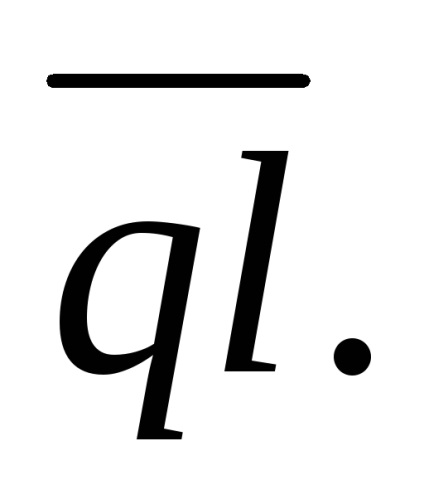
Ez a vektor irányított -q és + q (ris.11.6). Hatása alatt a külső mező orientálódni dipólus hajlamosak anyagokat, hogy azok elektromos pillanatok egybeesik az intenzitás a külső tér. A gyakorlati jelentősége természetesen nem egy dipólus és elektromos dipólus momentum (nagyon kicsi), és az összeg a villamos dipólusnyomatékkal vannak az egységnyi térfogatú, amely az úgynevezett polarizációs vektor
, azaz
A legtöbb dielektrikumok polarizációs vektor arányos a térerősség
és az arányossági tényező közötti elektromos nimik nevű fogékonyságot.
Amellett, hogy a vektoriális mennyiség a fenti
és
, fizikai jelentését, amely azt találtuk Térelméleti a számítás a vektort bevezetjük tovább
, nevezett elektromos elmozdulásvektorból vagy elektromos indukciós vektort. Ez a következőképpen definiálható: ahol
Ez az úgynevezett relatív dielektromos állandója a közeget, amelyben a mező jön létre, és
abszolút dielektromos állandója a közeget, amelyben a mező keletkezik.
Ez azt mutatja, hogy hány alkalommal az elektromos tulajdonságait a közeg eltérő tulajdonságai a vákuum (ez a különbség miatt előfordul, hogy polarizáció). Minden média
Ez határozza meg kísérletileg, és adjuk meg a kézikönyvekben.
Gauss-tétel
Gauss-tétel egy alapvető jog az elektrosztatikus mező. Azt találták kísérleti és matematikai írva
áramlási elektromos elmozdulásvektorból bármilyen zárt felületet körülvevő egy bizonyos térfogat megegyezik az algebrai összege szabad töltések, belső felületét (összesen
díjakat hozott a táblákat). mint
az
. A homogén és izotróp média
Ez egy állandó és lehet kivinni az integrál, akkor
Érdekes, hogy az áramlás vektoraD vagy E attól függ, csak
és nem függ a helyzet a töltés belsejében a zárt felület. Takarmány vektoraE létre nem csak szabad, hanem a kapcsolódó díjakat. Az utóbbit nem lehet figyelembe venni a
, és külön-külön vett a megkötött díjak, majd a képlet a Gauss-tétel a következő:
Ez a három képletek szerves formában felvétel Gauss-tétel, amely a nagy hatékonyság és az egyszerűség lehet kiszámításához használt térerő bármikor, ha miután ő is végezzen egy zárt felület, amelynek pont ugyanolyan körülmények kapcsolatos díjak, létrehozása terén. Példaként számoljuk területén előállított ponttöltés.
Egy pont az úgynevezett töltés található a test nagyon kicsi geometriai méreteinek. A ris.11.7 ő pedig egy pont (innen a név). Tegyük fel, hogy ez a töltés pozitív és található egy olyan környezetben, állandó
. Vegyünk egy tetszőleges pontján rasstoyanier bizonyos távolságban egy pont ellenében. A feszültség ezen a ponton fog irányulni mentén sugárirányú vonal (lásd ábra. Ris.11.7). A maga számítási képlet alkalmazandó
Erre a célra, húzunk egy megadott ponton keresztül egy zárt gömb alakú felület központja egybeesik ponttöltés. Vector elemi felületi
felé a külső felületre merőleges (közelében található a kérdéses pont). Mivel a példánkban, vektorok és DS azonos, akkor a termék megfelel a termék modulokat. Szintén minden pontján ezen a területen az érték a vektor E ugyanaz a szimmetria. Ezzel azt mondta, hogy van, mivel az a gömb felszínén van
Az összeg a szabad töltések adják csak ponttöltés
. Behelyettesítve ezeket az értékeket a képlet Gauss-tétel, megkapjuk:
Így ez a mező erőssége fordítottan változik proportsionalnor 2.
Proizvedom számítási kapacitása ezen a területen, képlet alapján
. Ha figyelembe vesszük, hogy a feszültség, és ennek következtében, a lehetséges attól függ, csak a sugár, az utóbbi képlet átírni
ebből az következik, hogy a kapacitás ezen a területen fordítottan arányos r. Az integrációs konstans A függ, hogy hol keresse a pont nulla potenciál.
Az integrált formában a Gauss-tétel nem ad választ a kérdésre, hogy hogyan lehet kapcsolatba lépni a térerőt, hogy pont a töltés ezen a ponton. A válasz erre a kérdésre, amelyet a differenciális alakja ennek a tételnek, ami következik integrál. Mert ez a kifejezés
osztja azt a térfogat által határolt felületre integrációs
Ez az összefüggés érvényes minden nagyságú kötetet. Hagytuk, hogy a nulla (azt mondják, hogy a szerződés a felület egy bizonyos pontig). TogdaPredel kapcsolat vektoraD átfolyik egy zárt felület határoló egy bizonyos térfogatot, hogy az értéke a térfogatot nevezzük divergenciáját vektor D (
) Vagy forrásra, illetve eltérés. A jobb oldalon az utolsó egyenlőség egy ingyenes sűrűsége zaryadaρsv. majd
Ez Gauss-törvény differenciális formában. Ennek lényege az a magyarázata, a támogatás három esetben tükröződik ris.11.8. Ha a vizsgált területen pont térfogatsűrűsége a szabad töltés pozitív, akkor az infinitezimális mennyiség, amely körülvesz egy adott pont, vonal vektoraD származnak (forrás pozitív, a különbség pozitív, pozitív divergencia). Ha a vizsgált pont a területén a szabad negatív töltés térfogatsűrűségű, az infinitezimális mennyiség, amely körülvesz egy adott pontján a vektor D sor tartalmaz (negatív forrás, a különbség negatív, a negatív divergencia). És végül, ha a kérdéses pont nem ingyenes, akkor ezen a ponton nincs lefolyó vagy a forrása a vektor vonalak D. hogy egy pont a vektor vonal D nem kezdődik és végét, és a permeátum infinitezimális mennyiség, amely körbevesz egy adott pont.
mint
az
A homogén és izotróp média
Ez egy állandó és lehet kivinni znakdiv. akkor azt kapjuk:
Ha figyelembe veszik a jelenség a polarizáció révén kapcsolódó díjak, az utolsó kifejezés lehet átírni
gdeρ
Us - térfogatsûrûsége kötött díjakat. Kihagyva a levezetése a kifejezést
, írni, hogy a derékszögű koordinátarendszerben
ez jelenti a részösszegként vektoraE nyúlványok mentén három tengely. Megmutatjuk, hogy a skalár szorzata nabla üzemeltető és a vektor E vesz egy eltérést az utóbbi:
Ezért Gauss-tétel differenciális formában gyakran írják, mint
Kapcsolódó cikkek