A medián Egy háromszög magassága, háromszög
Milyen következtetést lehet levonni, hogy a medián a háromszög magassága.
Ha a medián Egy háromszög magassága, ez a háromszög - egyenlő szárú.
CF - magasság és az átlagos
Δ ABC - egyenlő szárú.
Először felvázoljuk a bizonyíték. Ami azt jelenti, hogy a háromszög egyenlő szárú? Ez azt jelenti, hogy két oldal egyenlő. Tehát meg kell bizonyítani, hogy Δ ABC két oldal egyenlő: AC = BC. Az egyenlő felek következik egyenlő háromszögek. Ezért kell bizonyítania, hogy a két háromszög. Mi az? Δ AFC és Δ BFC.
Mi tudjuk, hogy a problémás nyilatkozat? CF - a magasságot, majd CF merőleges AB, úgy, hogy a szögek AFC és BFC - vonalak.
Még tudjuk, hogy CF - medián. Tehát ő osztja AB oldalán két egyenlő részből áll: AF = BF. Így két három pontot kell bizonyítania, hogy a háromszögek már van.
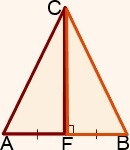
Ez a technika lehetővé teszi, hogy látni, hogy a CF oldalon - összesen.
Három pont ott.
Mi jár a felvétel bizonyíték.
Tekintsük Δ AFC és Δ BFC.
1) ∠AFC = ∠BFC = 90º (mivel CF - magassága ABC háromszög állapot).
2) AF = BF (mivel CF - medián ABC háromszög által feltétel).
3) Side CF - összesen.
Ennélfogva, Δ AFC = Δ BFC (két oldala és a köztük lévő szög).
A egyenlőségét háromszögek magában foglalja az egyenlőség az érintett felek: AC = BC. Ennélfogva, Δ ABC - egyenlőszárú AB bázissal (ahogyan azt az egyenlő szárú háromszög).
QED.
Ha a magassága a háromszög és minden medián egybeesnek, akkor a háromszög - egyenlő oldalú (minden két oldal egyenlő egymással, tehát mind a három oldal egyenlő).