A mechanikus relativitás elve 2
mechanikus relativitás elve. Galileo átalakulás.
A klasszikus mechanika, valós mechanikai relativitás elve: a jogszabályok dinamika azonos minden inerciális referencia rendszereket.
Tekintsük két keretet: inerciális rendszer K (koordinátái x, y, z), hagyományosan rögzítettnek feltételezzük, és a rendszer a K „(x koordinátáit”, y „z”), mozgó képest egyenletesen és lineárisan sebesség υ0 ( υ0 = const)
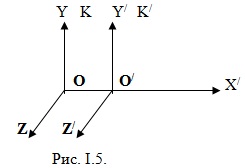
Koordinátája A pont tekintetében a keret K: x = x „+ 00”, egy időintervallum t a származási lenne:
Egyenleteket (3.19) nevezik a koordináta-transzformációt és a Galileo időben. A visszaszámlálás megkezdődött az idő, amikor az eredete a két rendszer megegyezik. Differenciálás adott időben t, megkapjuk az expresszióját sebesség mellett szabály klasszikus mechanika: υ = υ „+ υ0 (3,20)
Gyorsulások mindkét keret azonos, ami azt jelenti, hogy a viselkedését a szervek mindkét rendszerben azonos: a = a „(3,21), azaz a kapcsolatban (3,21) következik megerősítését mechanikai relativitás elve: egyenlet dinamikájának az átmenet az egyik inerciális referencia rendszer egy másik nem változott, azaz Ezek invariáns képest Galilei-transzformáció. A mechanikai relativitás elve is formálhatjuk a következőképpen: semmilyen mechanikai kísérletek, végzett a Inerciarendszer, lehetetlen megállapítani, hogy ez nyugalomban vagy mozgó egyenletesen egy egyenes vonal. Például ül a kabinban a hajó mozog egyenletesen egy egyenes vonal, nem tudjuk meghatározni a hajó pihen, vagy mozog, nem nézett ki az ablakon.