A kanonikus alakja lineáris programozási feladat
Általában a lineáris programozási feladat rögzítésre kerül, így, hogy a korlátozások, mint egyenletek és egyenlőtlenségek, valamint a változók lehetnek mind a nem-negatív és önkényesen változó. Abban az esetben, amennyiben a megszorítások egyenletek és az összes változó eleget nemnegativitását, a lineáris programozási probléma az úgynevezett kanonikus. Meg lehet képviselve egy koordináta, egy mátrix vagy vektor formájában.
1. A kanonikus lineáris programozási feladat egy koordinátát a formája
.
A tömörebb, ez a probléma lehet írni az összegzés jele,
2. A kanonikus lineáris programozási probléma vektor jelölése a formája
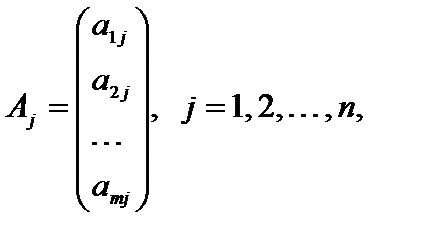
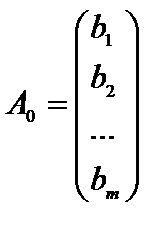
3. A kanonikus lineáris programozási probléma mátrix jelöléssel formában van
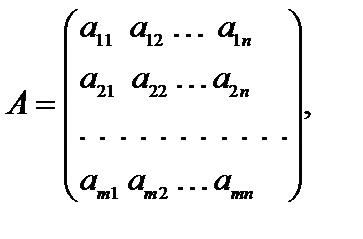
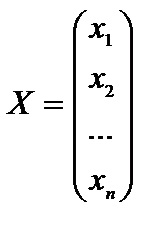
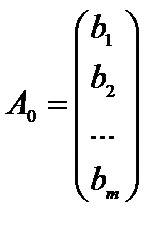
Itt, A - mátrix együtthatók az egyenletek, X - oszlop mátrix probléma változó, - oszlop mátrixa jobb oldalán restrikciós rendszer.
Gyakran használják a lineáris programozási feladat, az úgynevezett szimmetrikus. amelyek formájában mátrix jelöléssel
1.4. Csökkent az általános probléma a lineáris programozás
kanonikus forma
A legtöbb megoldási módjait, lineáris programozási feladatok feltételezik, hogy a korlátozást rendszer áll egyenletek és természeti feltételeinek nemnegativitását változók. Azonban az előkészítés matematikai modellek a gazdasági problémák korlátozások elsősorban kialakítva a rendszer egyenlőtlenségek, így képesnek kell lennie arra, hogy mozogni egyenlőtlenségrendszer az egyenletrendszert. Erre a célra, azt bizonyítja a következő tétel.
1.1 Tétel. Ahhoz, hogy cserélje ki a egyenlőtlenség egyenletet. Minden döntés egyenlőtlenség
Ez megfelel egy egyedi megoldás
és fordítva, minden egyenlet megoldása (1,13) és az egyenlőtlenség (1.14) megfelel az egyetlen megoldás a (1.12).
Bizonyítás. Let - az oldatot a (1,12), majd a. Jelöljük a különbség a jobb és bal oldalán ez az egyenlőtlenség keresztül. t. e.
.
Nyilvánvalóan. Behelyettesítve egyenlet (1,13) helyett a változó értékeket. megkapjuk
.
Így kielégíti az egyenletet (1,13) és a egyenlőtlenség (1.14). Tehát az első része a igazolást a tétel.
Tegyük fel, hogy kielégíti (1.13) és az egyenlőtlenség (1.14), t. E. Have
Elöntve a bal oldalon az egyenlet nem negatív érték. kap
,
t. e. kielégíti az egyenlőtlenség (1.12). Ez azt bizonyítja, a tétel.
Ha az egyenlőtlenség. A további nem-negatív változót kell beírni a bal oldalán egy mínusz jelet, t. e ..
Nem negatív változók be a egyenlőtlenség korlátokat át őket az egyenlet, az úgynevezett kiegészítő változókat. További változók lépett az objektív függvény nulla együtthatók, és ezért nem befolyásolja az értékét.
Abban az esetben, ha a probléma önkényesen változó változók, akkor az ilyen helyettesítő változó különbség a két nem-negatív változók r. F .. hol.
Néha el kell menni a problémát találni a minimum, hogy a meghatározott maximális, és fordítva. Ez elég ahhoz, hogy változtatni a jelek minden együttható a célfüggvény a másik, mint a többi probléma változatlan marad. Optimális megoldás ily módon kapott problémái maximumok és minimumok egybeesnek, és az értékeket a célfüggvény optimális megoldás csak abban különböznek jel.
Példa 1.1. Vezet a kanonikus alakja lineáris programozási feladat.
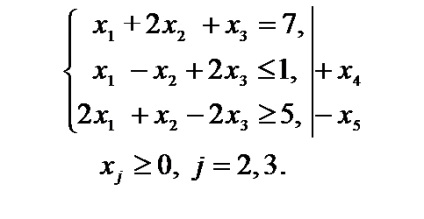
Határozat. Térjünk át a probléma megtalálni a maximális célfüggvény. Ehhez megváltoztatjuk a az együtthatók előjelei a célfüggvény. Az átalakítás az egyenletek a második és a harmadik egyenlőtlenségek korlátok a rendszer, amit be további változók nem negatív (a matematikai modellben a művelet betűvel E). Változó bekerül a bal oldali részén a második egyenlőtlenség a „+” jel, mivel az egyenlőtlenség adni. A változó be van dugva a bal oldalon a harmadik egyenlőtlenség a „-” jel az egyenlőtlenség formáját ölti. A célfüggvény változók által bevezetett olyan tényező nulla. Változó. amely nem által előírt feltétel nem negativitás helyébe a különbség. . Írja be a feladatot a kanonikus alakban
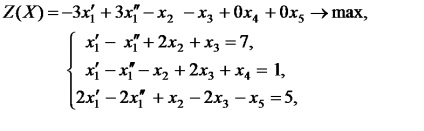
.
Bizonyos esetekben szükség van ahhoz, hogy a problémát a kanonikus szimmetrikus problémát. Vegyünk egy példát.
1.2 példa. Vezet szimmetrikus forma lineáris programozási feladat
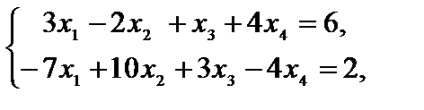
.
Határozat. Gauss-Jordan módszerrel csökkenteni az egyenletrendszert korlátozott feladatokat az egyenértékű megengedett. Ugyanakkor engedélyezett ismeretlen kizárni a célfüggvényt. Erre a problémára megoldás a táblázatban (1.1.) Együtt az együtthatók a kényszer egyenletrendszer egy további sort levelet célfüggvény együtthatók. Az utolsó oszlopban a kiegészítő vonal (helyett a jobb oldalon egyenletek), írunk a szabad kifejezés a célfüggvény értéke nulla. A számítások figyelembe veszik, hogy a felbontás elem az utolsó sorban (a célfüggvény) nem választható.
T a b L E 1.1
Száma -9 kapott az utolsó sorban az utolsó oszlop a táblázatban, írásban kell célfüggvény ellentétes előjelű. Ennek eredményeként ezek az átalakulások, a probléma a következő alakban:
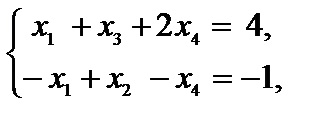
.
Mivel a változók nem-negatív, elutasító velük, tudjuk írni a feladatot a szimmetrikus forma
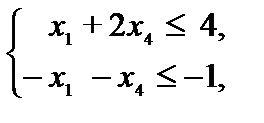
.