A fő alkalmazási a származék
Sebesség és gyorsulás
Legyen a függvény \ (k \ left (t \ right) \) leírja a helyzetét egy objektum egy koordináta-rendszerben időpontban \ (t \). Ezután az első függvény deriváltját \ (k \ left (t \ right) \) a pillanatnyi sebesség az objektumot:
\ (V = s ^ = f „\)
A második derivált függvény \ (s \ bal (t \ right) \) képviseli a pillanatnyi gyorsulását az objektum:
\ (W = v ^ = s ^ = f '' \)
Az egyenlet az érintő
\ (Y - = f ^ \ prime \ right)> \ right)>, \)
ahol \ (\ left (, \ jobbra) \) - koordinátáit a fogási pontot, \ (f ^ \ prime \ right)> \) - értéke differenciálhányados \ (f \ left (x \ right) \) át az érintési pont.
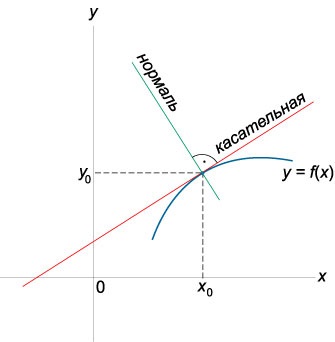
ahol \ (\ left (, \ jobbra) \) - a koordinátáit a pontot, ahol végzett a normális, \ (f ^ \ prime \ right)> \) - értéke differenciálhányados \ (f \ left (x \ right) \) a ebben a kérdésben.
Növekedése és csökkenése funkció
Ha a \ (f \ left (> \ right)> 0 \), akkor a függvény növekszik a ponton \ (\). Az alábbi ábra egy olyan növekvő függvény a \ (x \).
Ha a \ (f \ left (> \ right) 0 \)) minden \ (x \) egy bizonyos intervallumban \ (\ left (> \ right] \) és csökkenti (\ (f \ left (x \ right ) 0 \)) az összes \ (x \) intervallumban \ (\ left [, b> \ right) \), akkor a függvény \ (f \ left (x \ right) \) van egy lokális minimum a ponton \ (\ ).
A második elegendő feltétele a létezését szélsőérték
Ha a \ (f '\ left (> \ right) = 0 \) és \ (f' „\ left (> \ right) 0 \), akkor a függvény \ (f \ left (x \ right) \) van egy helyi minimum pontnál \ (\).
konvex függvények
Funkció \ (f \ left (x \ right) \) konkáv (vagy konkáv) azon a ponton, \ (\), ha a származék \ (f „\ left (x \ right) \) ezen a ponton csökken (rés \ ( x \)).
Elégséges feltételei konvexek felfelé és lefelé
Ha a \ (f '' \ left (> \ right)> 0 \), akkor a függvény \ (f \ left (x \ right) \) van lefelé domború pontnál \ (\).
Ha a \ (f '' \ left (> \ right)