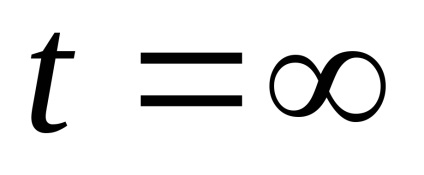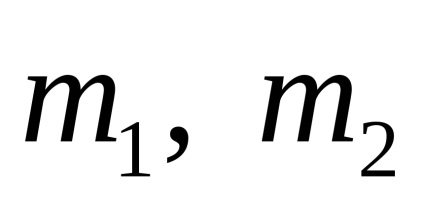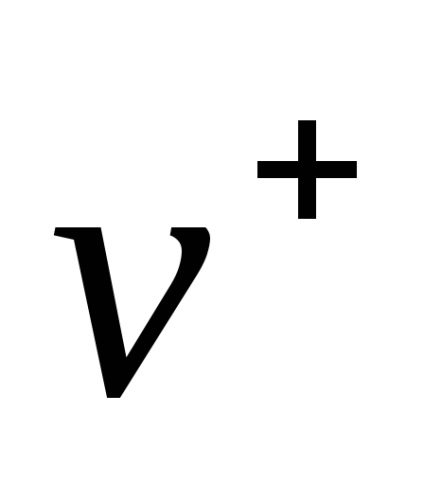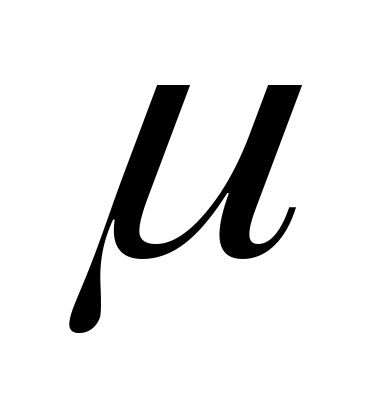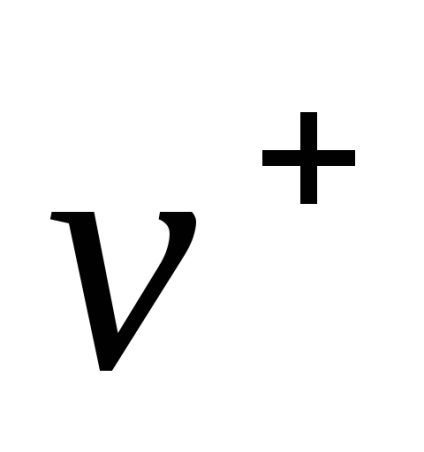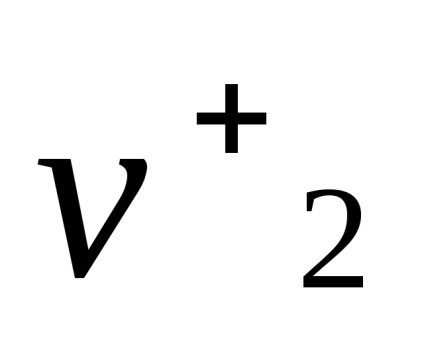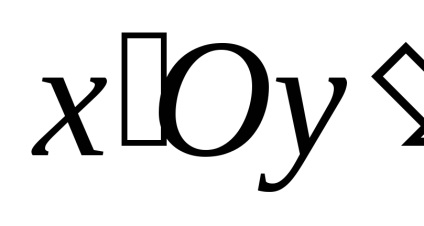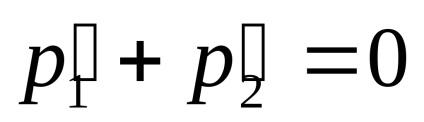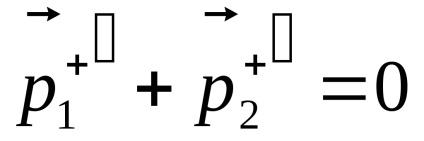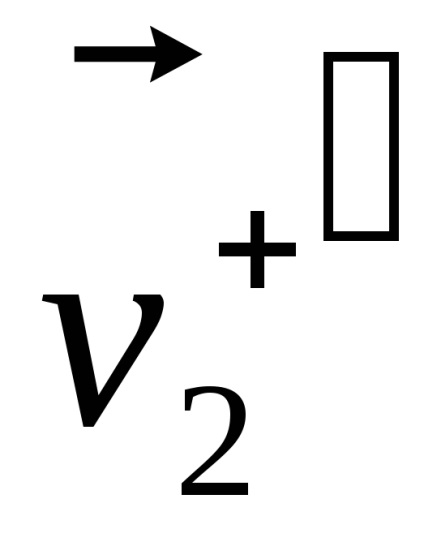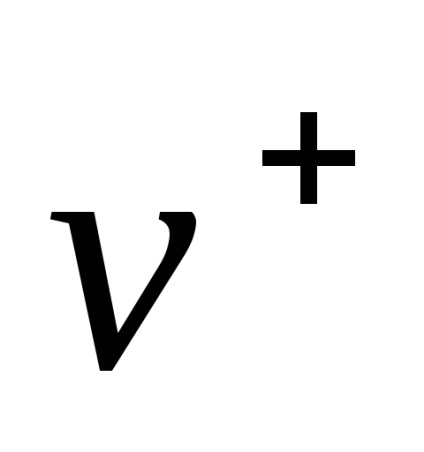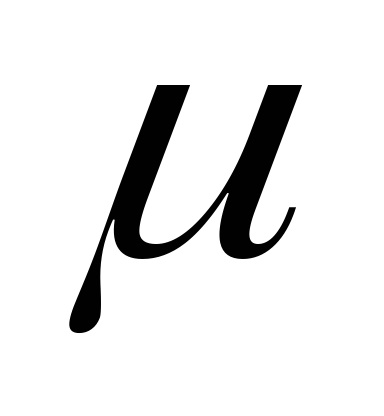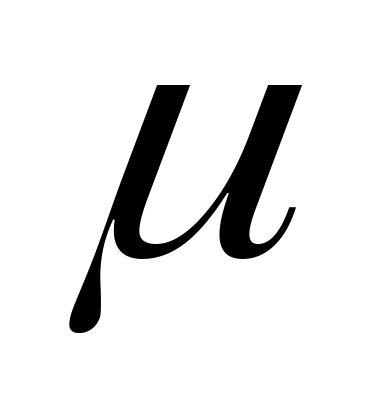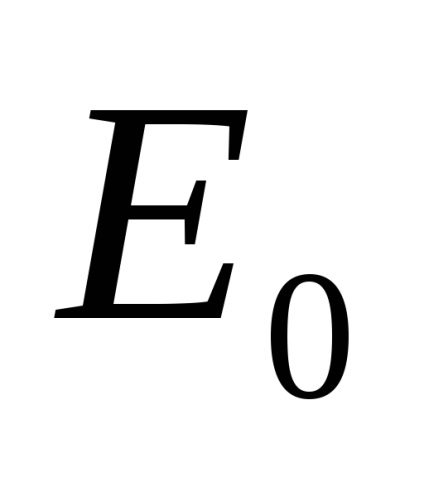6.1. Általános nyilatkozat a probléma
A elméleti mechanika belül két test probléma megoldódott alapvetően két problémát: meghatározásának problémáját az energia értékeit a rendszer, a részecske pályái mozgó korlátozott régióban a tér, és a probléma a fényszóró részecskét, amely magában foglalja a tanulmány a rugalmas szórás. Két fényszóró részecskék, úgynevezett rugalmas ha ez a folyamat nem változik, az állam a kölcsönható részecskék.
Készítmény a szórási probléma a következő. Először is, kényelmes, hogy vállalja a kezdő időpontja
. Azt feltételezik, hogy a
A részecskék nem lépnek kölcsönhatásba (szabadon), mivel ezek végtelenül távol egymástól, és ezért azok kölcsönhatási energia, csökkenő függvénye a köztük lévő távolság nulla. Ezután a részecskék kölcsönhatásba lépnek egymással, de amikor
diszpergáiódjanak nagy távolságokra, valamint azok kölcsönhatását energia ismét eltűnik.
A cél az, hogy meghatározzuk a mechanikai állapotát egy olyan rendszer, amely részecskéknek
, kérve őket, hogy jelezzék,
. A kvantummechanika államok a részecskék
In-hívásállapotot, míg
- Out-államokban. Célszerű, hogy kövesse ezt a terminológia és elméleti mechanika. Ez könnyen belátható, hogy a mechanikai állapotát egy olyan rendszer, amely két részecskék,
és
Ez határozza meg a sebességet (vagy impulzus), így a vektorok jellemzése In-state vektorokat és államilag Out-Systems. Ezen kívül meg kell adnia a részecskék tömegének
, kölcsönhatásuk energia
és beállítás
, Ez az úgynevezett észlelési távolságot.
A részecskék sebessége viszonyítottak egy tehetetlenségi referenciához rendszer, amely a szóráselmélet nevén laboratóriumi rendszer vagy n -rendszer. Ha figyelembe vesszük a problémát, a szórás a két részecske gerendák (ebben az esetben azt feltételezzük, hogy az egyik gerendája minden részecske azonos tömegű, mondjuk
, és sebesség
, és a második
és
akkor, mint később látni fogjuk, az egyik is be kell állítani a szöget
meghatározza a tájékozódás a síkban mozgás mindegyik pár a vonatkoztatási rendszer kapcsolódó tömegközéppontja vagy egy pár (ez a rendszer az úgynevezett N-rendszer).
Két részecskék szórási probléma megoldható általános formában, a kapott oldatot a fenti problémát a két test. Tény, hogy a két test probléma, csökkentheti a problémát a mozgás
-ponttól kezdve, mivel a megőrzése a tömegközéppontja a rendszer sebességét a szórási folyamat (mert az izolált rendszer) találunk
ahol
- a tömegközéppontja sebesség, és a
sebesség
-pont után a szórás. érték
Találunk a törvény az energiamegmaradás az
-pont (a törvény az energiamegmaradás a két test képest a c-rendszer):
De ettől. ezért
, ahol
, és a készülék vektor
rendező
vagy
.
A szórási folyamat az N -rendszert lehet grafikusan (ábra. 1.6) egy síkban
, amely a sík mozgás a kölcsönható részecskék. Emlékezzünk vissza, hogy ha
ábra szerinti. 1.6, akkor szerint a (38,5)
,
ahol
-sugár - vektor
-pont.
Mivel u S rendszer egy adott időpontban
(És ezért
és
) Közötti szög
és
egyenlő közötti szög
és
és így, a részecske sebessége bármely ponton
egymással ellentétes irányú. Így, az eredmény a rugalmas szórás részecskék csökken a n -rendszert a forgási sebességnél a maradó kétféle részecske kölcsönösen átellenesen és változatlan nagyságú. De mivel a vektor
párhuzamos
, Ez a szög megegyezik a hajlásszöge
-pont.
Jelöljük a hajlásszöge a levél
. Vesszük figyelembe, hogy a poláris szög
kifejezve a határozott integrál:
ahol a fordulópont
Ez a gyökere az egyenlet
.
A integrandus a (3.6) tartalmaz a jellemző paramétereket
-pont. Nyilvánvaló, hogy
Itt már használják egy közös tulajdonsága a szimmetria a pálya egyenes vonalat húzott a mező közepén pontjához legközelebb a pályára. Ezért mind a asymptote pályára mondják,
-pont metsző elrendezésű egyenes azonos szögben. szög
az úgynevezett szórási szög a cms; ez egyenlő a szög a két aszimptotákkal a röppálya
-pont, és
- közötti szög a röppálya és aszimptotájának apsidal vektort.
A próba távolság - a távolság a aszimptotái a részecske pályák a n -rendszert, amelyen keresztül a részecskék mozognak a szórás. Azt is meg lehet meghatározni, mint a minimális távolság, amelynél a részecskék telt egymást hiányában a kölcsönhatás közöttük.
A probléma a szórási megmaradó mennyiségek
és
Általában írta a sebességet
és a hatása paraméter
:
,
mivel Ez azt mutatja,
a hossza merőleges csökkent a központ területén a röppálya aszimptotával
-pontot, vagy azzal egyenértékű, a legkisebb távolság, amelynél
-pont haladna a központtól, ha a kölcsönhatás, és a mező így teljes egészében hiányozhat.
Képletek (1.6) és (4.6), az oldat a probléma a rugalmas szórás a két részecske. Látjuk, hogy ez a probléma csak egy speciális esete a két test probléma, ha ez szükséges ismerni csak a sebesség a részecskék az ütközés után a
. rasi
Ez csak attól függ,
,
, valamint a típusú kölcsönhatás és a részecskék között a paramétereket, amelyek jellemzi, azaz a -tól