4Oborot mayatnik1
I. Összefoglaló elmélet
F
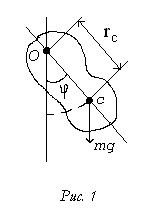
Jelöljük a távolságot rc a forgástengelytől a tömegközéppont. Pendulum, mérlegen helyzetben lenne oszcillál. A helyzet az inga, jellemezhető hajlásszöge (


Mozgás a test a rögzített helyhez képesti meghatározott tengely pillanatok egyenlettel:
Pillanatban a külső erők Mvnesh áll gravitációs pillanat
és a súrlódási nyomaték. Gyakran előfordul, hogy egy durva közelítés, úgy gondoljuk, hogy a súrlódás elhanyagolható. Impulzusnyomatékhajtómű inga
ahol J - tehetetlenségi nyomatéka az inga viszonyított forgástengelye.
Figyelembe véve egyenletek (2) és (3) lendület (1) egyenlet átírható, mint:
Ebben az egyenletben, egy ismeretlen funkció függvénye - az inga eltérítési szög és annak ideje származékai: szögsebességgel és szöggyorsulás. (4) egyenlet érvényes minden rezgés amplitúdója az inga. Sokkal egyszerűbb a kis rezgések az inga, ha a szög eltérése az egyensúlyi helyzetből kicsi
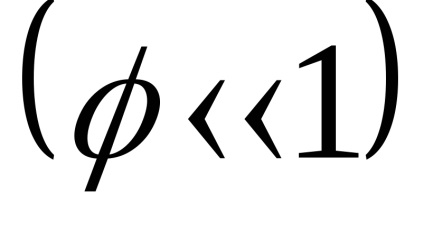
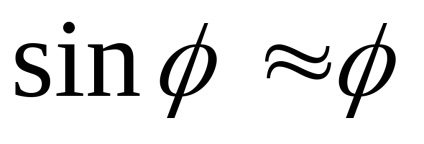
Másodrendű differenciálegyenlet (5) van egy oldat formájában:
ahol A - rezgés amplitúdója,
Meg fogjuk mutatni, hogy közvetlen helyettesítés
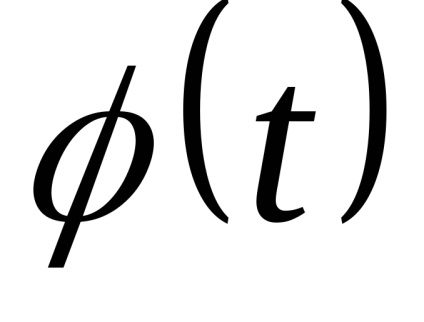
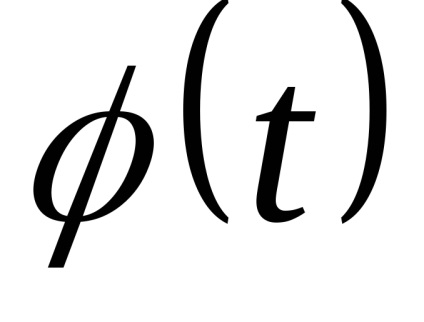
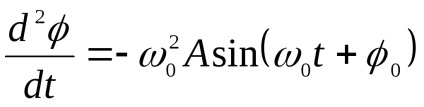
Mi helyettesíti ez a kifejezés (5)
A kapott összefüggés teljesül bármikor, feltéve, hogy:
Következésképpen, a körfrekvencia oszcillációs az inga
Az egyenlet a mozgás (

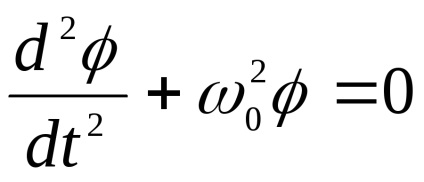
Oh
Az inga oszcillálni egy függőleges síkban, pihenő alsó széle egyik prizmák a rögzített hordozó felületén.
(7) egyenlet alkalmazható meghatározására gyorsulás szabadesés g. Ez megköveteli izmeritT, J, rc.
Egy működő inga (inga munkamódszer) lehetővé teszi, hogy meghatározza g szerint nem izmeryayaJ irc. Az a tény, hogy a két oldalán a tömegközéppontja az inga van egy munkahelyzet a támogató élek, amelyben időszakokban rezgések az inga egybeesik (lásd. Alkalmazás).
Jelöljük RC1 irs2 (RC1
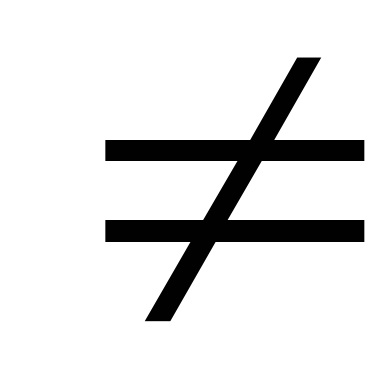
Mivel (7) egyenlet
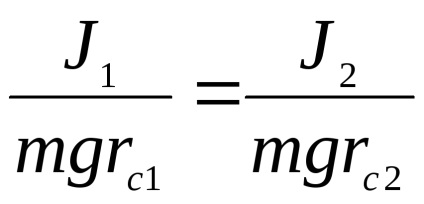
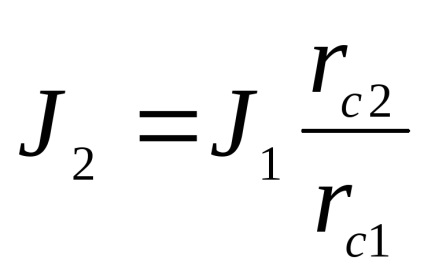
A tétel Steiner
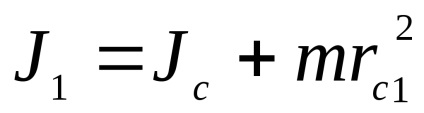
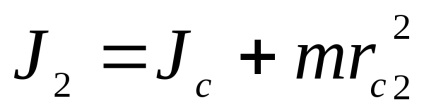
Az utolsó egyenletet ki tudjuk fejezni a tehetetlenségi nyomatéka az inga közepéhez képest a rezgő tömegek
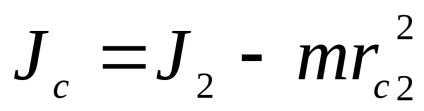
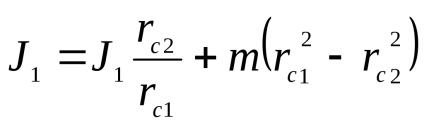
Definiálása J1 és helyettesítésével ezt a kifejezést itt
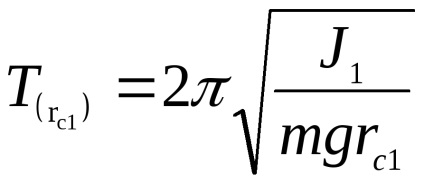
Pontosan ugyanez a képlet nyerhető
Következésképpen, a gyorsulás a szabadesés meghatározható a következő képlettel:
Ahhoz, hogy megtalálja gdostatochno intézkedés csak a két érték: távolság (RC1 + RC2) között az alátámasztó bordák és prizmák időszak inga lengési polozheniirc1 és a „fordított” polozheniirc2. Ez chtorc1
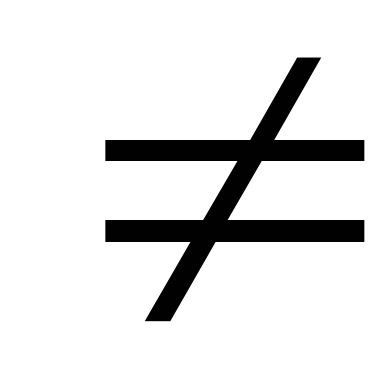
Feladat 1. Válogatás rasstoyaniyrc1 irc2. ahol
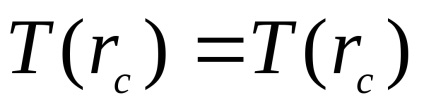
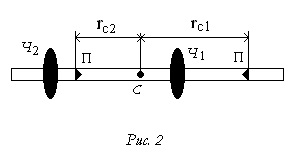
Mozgatható terhelés van rögzítve a rúd aszimmetrikus helyzetben (2. ábra): a terhelés - a végén a rúd, a másik - a magjában.
Körülbelül meghatározza a helyzetét a tömegközéppont az ingával. Az egyik jobb prizmák erősítette meg a legnagyobb, RC1 lehetséges távolságra a tömegközéppontja (közel a rúd vége). A második - a másik oldalon a tömegközéppontja ahhoz a ponthoz közel C. Ebben a helyzetben meghatározott ideig
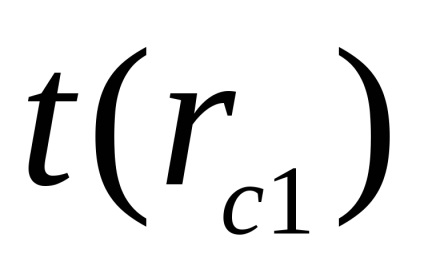
Ezután helyzetének megváltoztatása nélkül a rakomány (invertált inga), meghatározza az idő
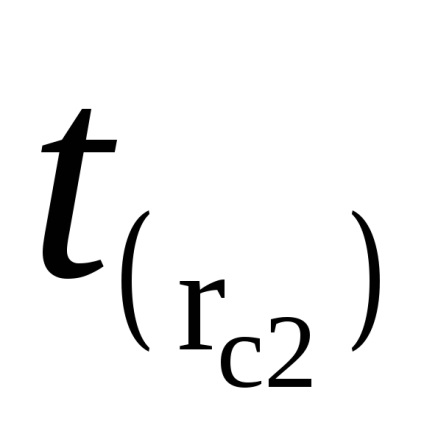
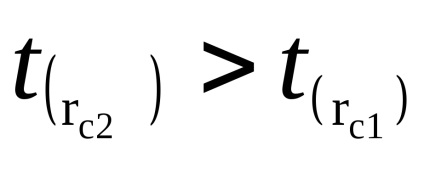
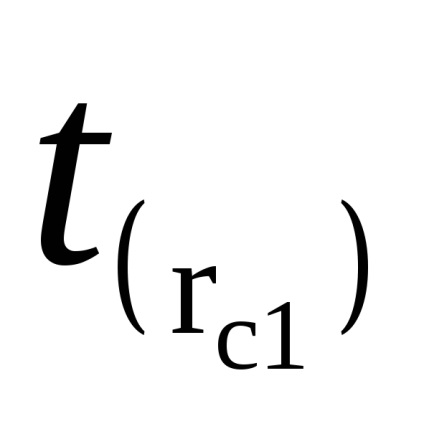
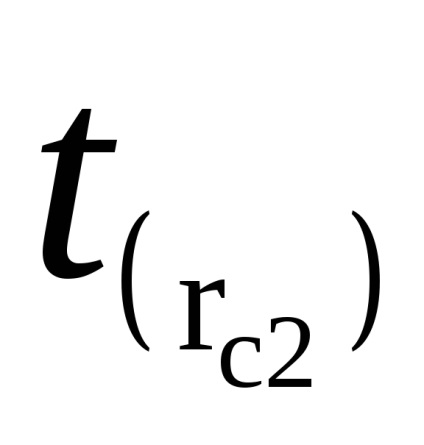
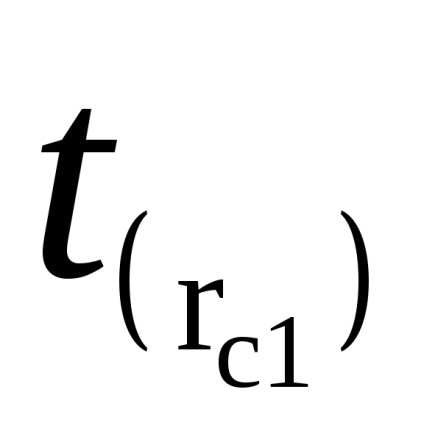
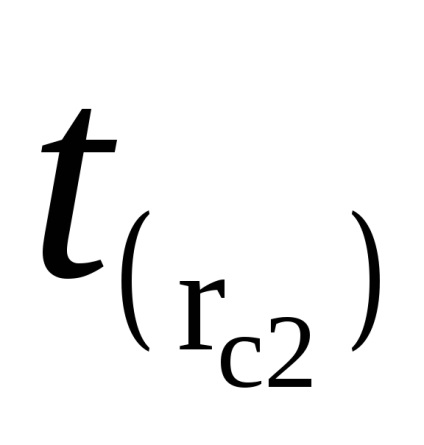
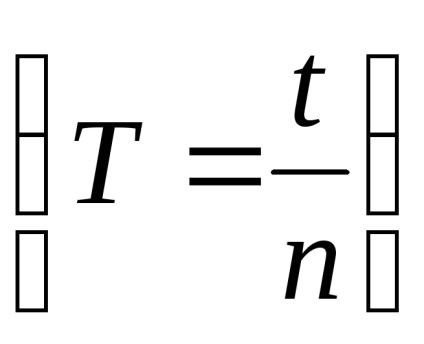
Feladat 2. meghatározása a gravitációs gyorsulás.
Határozza idő 50 oszcilláció (háromszor) t (RC1) és t (RC2). Töltse ki a táblázatot.
Mérjük meg a távolságot (RC1 + RC2).
Számítsuk nehézségi gyorsulás, amelyet a képlet (9).
Vedd műszer mérési hiba (stopper és vonalzó).
Számoljuk ki a relatív hiba levezetés eljárás, és meghatározzuk a megbízhatósági intervallum
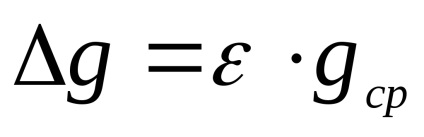
3. feladat meghatározása a helyzet az inga tömegközéppontja.
Ingás rúd hossza 1,25m, massamst = 0,260 kg; prizma súlya 0,22 kg és 0,175 kg; lencse súlya 0,930 kg és 1,44 kg.
Ezekből az adatokból és távolságok minden rakomány egyik végén a rúd (intézkedés) meghatározza az elméleti érték a tömegközéppont. Hasonlítsa össze a tömegközéppont talált érték kísérletileg az inga, amellyel a számítást végzünk, g.
Adjuk meg a fizikai mennyiségek: nyomaték, tehetetlenségi nyomaték, lendület szervek tengelyéhez viszonyítva; az irányba?
Fogalmazza meg a egyenlet pillanatok.
Kimenet képletű időszak lengésének fizikai inga.
Milyen értéket nevezzük csökkentett hossza a fizikai inga?
Mi a neve az inga forgatható? Előnye meghatározásakor g?
Képletek meghatározására gmetodom forgó inga.
Lehetséges, hogy meghatározzuk g segítségével a tétel a Steiner és ismerve a tehetetlenségi nyomaték
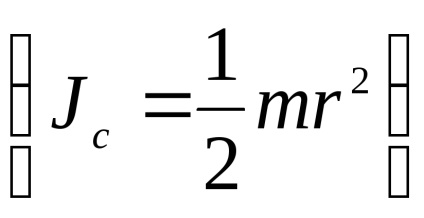
Által meghatározott abszolút hiba az oszcilláció időszakban.
Bármelyik van a laborban meghatározva kevesebb pontosság: T vagy (RC1 + RC2)?
Van-e értelme, hogy növelje a pontosság meghatározására teljes egyezés gdobivatsya ideig? Miért?
Bizonyítsuk be. Hogy amikor az oszcilláció időszakokra lehet tekinteni egyenlő 10 -3?
Attól függ, hogy az időszakok rezgés a fizikai dolgozó ingával súlyuk?
Szerezd meg a képlet meghatározására

Hogyan lehet azonosítani a tömegközéppontja az inga kísérletileg és elméletileg az ismert paraméterek az inga?
Sivukhin AV „Az általános tanfolyam fizika” V.1. Mechanics. M. 1976. pp. 166-170, 172-173, 209-213.
arkangyal MM „A kurzus a fizika.” Mechanics. M. 1975. pp. 297, 301-305, 315-316, 327-328.
Alekszandrov, NV Yashkin AY „A kurzus az általános fizika.” Mechanics. M. 1978. pp. 335-336.
Savelyev IV „Természetesen a fizika” V.1. Mechanics. Molekuláris fizika. M. 1989. pp. 101-107.
Gershenzon EM NN Malov „A kurzus az általános fizika.” Mechanics. M. 1979. pp. 85-89.
Egyik előnye az, munkamódszer az inga meghatározására gyorsulás szabadesés, hogy I0 irc nem szerepel a számítási képlet dlyag. Most viszont, hogy a vita ezzel a módszerrel.
Szerint a Huygens-Steiner-tétel, a tehetetlenségi nyomaték a inga tengelye körül O
ahol Ic - az inga a tehetetlenségi nyomaték egy tengely párhuzamos a swing tengelyére és áthalad a tömegközéppontja C az inga, rc - közötti távolság a tengely O és S.
Szállító (2) be (1) megkapjuk
Megbeszéljük minőségileg függését a rezgési periódus olyan távolságban rc a swing tengelyen. Nagyon malyhrc. súlypontja
M = -mgrc sin


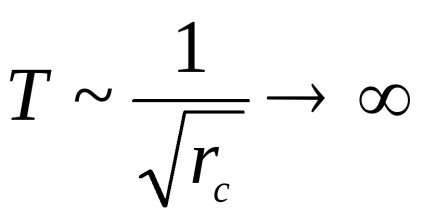
Az ellenkező határ nagyon nagy RC prenebrechIs képest CMR
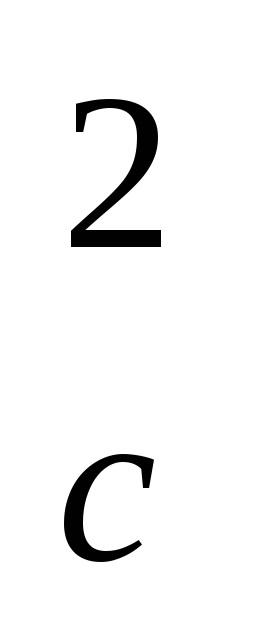
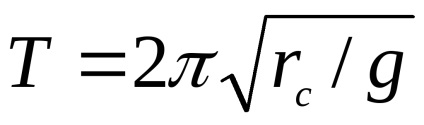
P

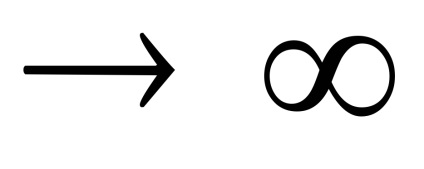
Érték rc = 0 megfelel a tömegközéppontja az inga. Ha az inga van függesztve, a másik oldalán a súlypont, amint az általános képletű (3), a függőség a T (RC) lesz pontosan ugyanaz. Ezért, a grafikon T (rc) két szimmetrikus ága megfelelő az inga felfüggesztési pont balra vagy jobbra a tömegközéppontja.
A grafikon azt mutatja, hogy minden egyes oldalon a tömegközéppontja az inga két helyzete megtámasztására prizmák, amelyben az inga oszcilláció időszakok egybeesnek.