№4 téma Előadás 2

konvex programozási feladat

2.1.1. A koncepció egy konvex halmaz

Definíció. MnozhestvoS

En nevezzük konvex, ha bármely két pont és van

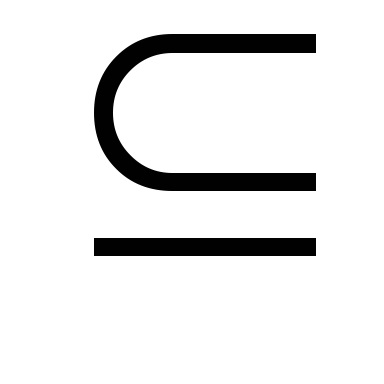
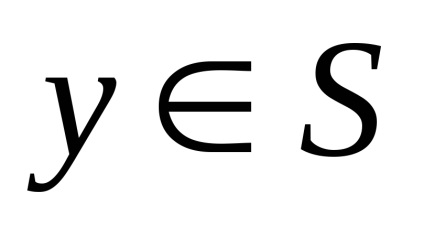
bármikor

. Geometriailag, ez azt jelenti, hogy együtt és és az egész szegmens Tartozik a beállított . Megjegyezzük, hogy a szegmens az úgynevezett konvex kombinációja pont és .

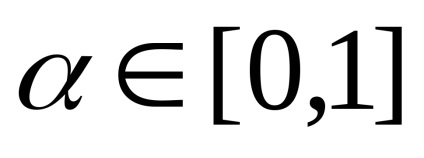
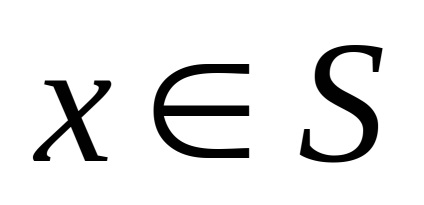
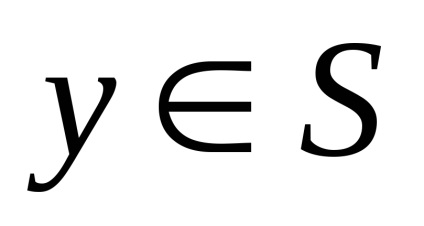
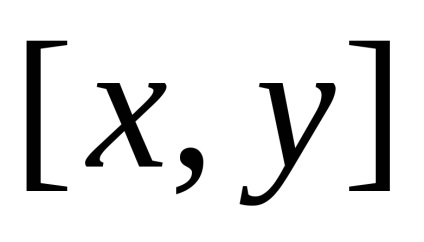
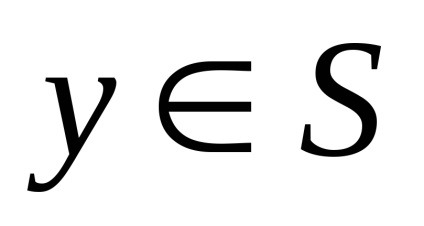
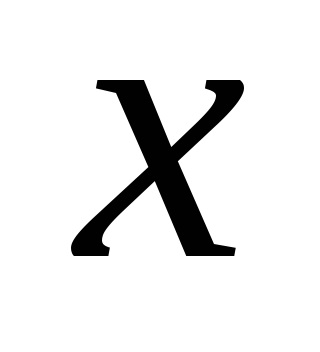
Példák konvex halmazok

2. Az üres halmaz.

3. A szett tartalma egypontos

,

,

ahol

, a ≠ 0 és b - számát. N = 3 van beállítva egybeesik a normális síkkal, és az N = 2 - egy egyenes vonal.

,

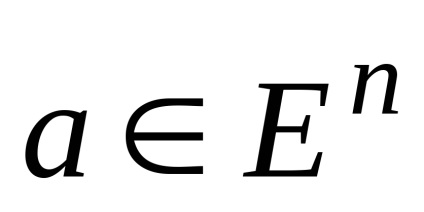
ahol

, a ≠ 0 és b - számát.

,

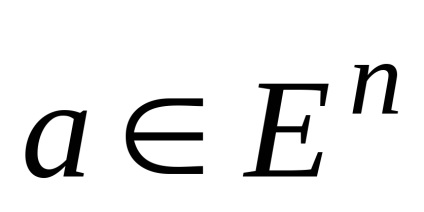
és y (k) - megadott vektorok

. Megjegyezzük, hogy gyakran nem tekintik a kúp csúcsa az origó, és bármely más ponton . azaz egy sor típus

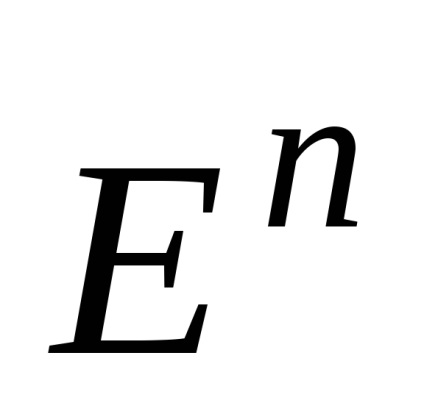
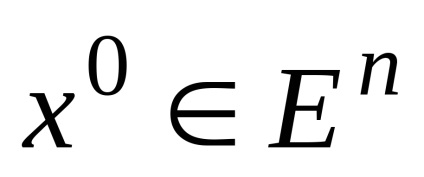
7. A konvex kombinációja (Shell) véges számú pontot

.

Egy ilyen sor geometriailag jelentése n-dimenziós konvex politóp.

8. A találkozásánál véges számú fele

,

hol. Ez a készlet az úgynevezett poliéder konvex halmaz. Abban az esetben, ha az arra korlátozódik, ez is egy konvex poliéder. Tehát van két lehetőség ábrázolásai konvex poliéder - formájában konvex burka egy véges ponthalmaz és véges számú találkozásánál félig terek által meghatározott egyenlőtlenségeket.

9. Ball r sugarú ≥0 középpontú

.

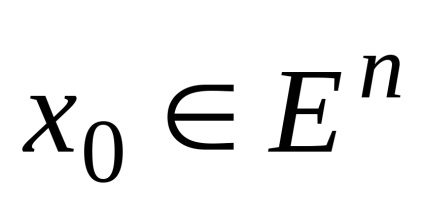
Példaként említhetők a nem-konvex halmazok több egész számok vagy a racionális számokat.

2.1.2. A tulajdonságait konvex halmazok

A kereszteződés bármennyi konvex halmazok konvex halmaz.

Az unió két konvex halmazok nem feltétlenül konvex.

Példa: az unió a két pont konvex halmaz.

geometriai összege

. Két konvex halmazok és. meghatározása

,

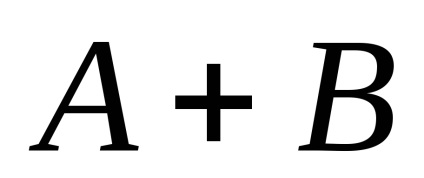
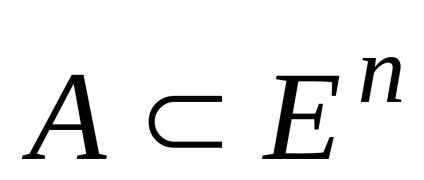
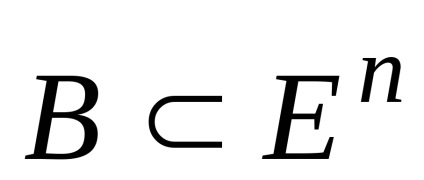
Azt is konvex.

Artwork konvex halmaz

A chisloα. meghatározása

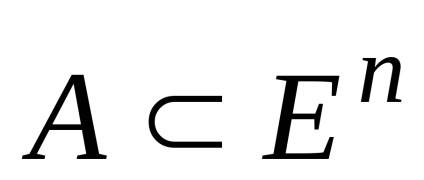
Azt is konvex.

Ezek a kijelentések következnek a meghatározása a konvex halmaz. Lássuk be, például az első nyilatkozata a kereszteződésekben a két

és. Let. Tekintsük

.

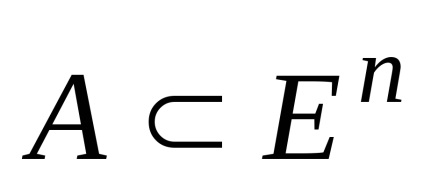
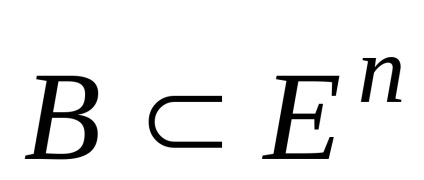
A konvex és B kapjuk, hogy

és minden . Itt van. Az az állítás bizonyított.

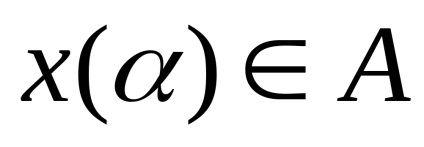
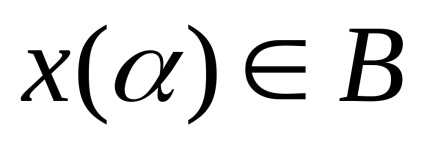
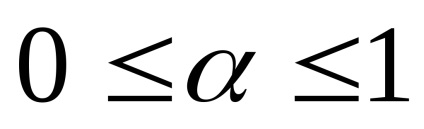
Meghatározása .Krayney (extremális) pont konvex halmaz, ez az úgynevezett egy pont, amely nem képviselheti egy konvex kombinációja két különböző pontjain ezt meg.

Példaként, egy konvex poliéder. A szélsőséges pontok a csúcsot.

Definíció. MnozhestvoS

En nazyvaetsyastrogo konvex. ha konvex és annak minden határpontokhoz szélsőséges.

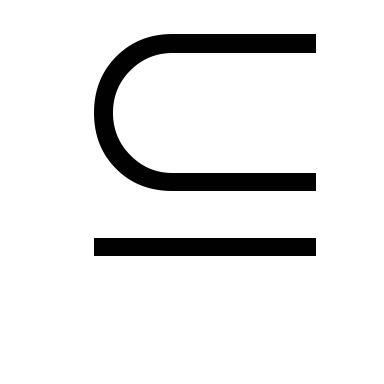
Egy példa a szigorúan konvex halmaz zárt el.

2.1.3. támogató hipersíkot

Tekintsük a legfontosabb fogalom a támogatási hipers'ık. Először is jegyezzük meg, hogy hipersíkot. ahol

, a ≠ 0, meghatároz egy teret két zárt fél-terek

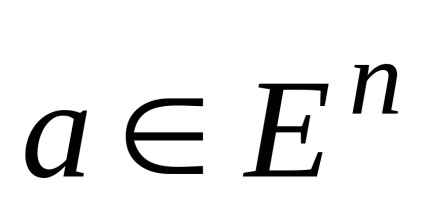
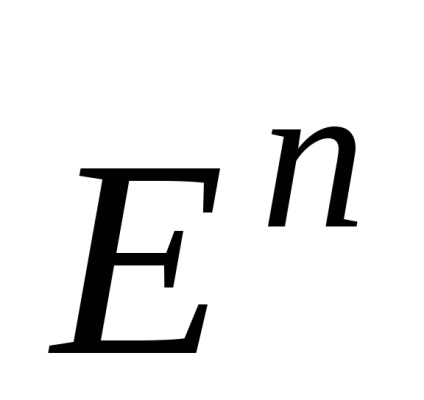
Hipersíkot a metszéspontja ezeknek fele-terek, míg a határ mindegyik.

Tegyük fel, van egy konvex halmaz S és annak határán tochkay.

Definíció. GiperploskostH. áthaladó tochkuy, és tartalmazza az összes pontot az egyik mnozhestvoS általa meghatározott zárt felében hívják hipers'ıkot támogatásának mnozhestvuS a tochkey.

Belátható, hogy a támasz hipersík segítségével lehet bármely határpont egy konvex halmaz. Illusztráció alátámasztó hipersíkot ábrán látható. 3.1.

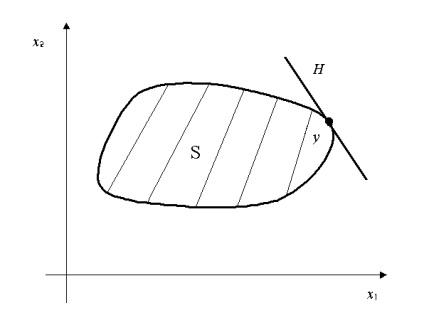
Ábra. 3.1. Referencia hipersíkot H egy konvex halmaz S ponton y.

Megjegyezzük, hogy a támogatás hipers'ık lehet, nem egyedi (lásd. Ábra. 3.2).

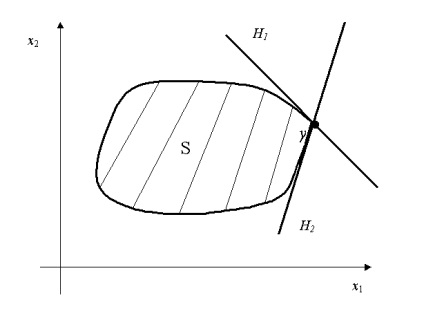
Ábra. 3.2. Két referencia hipersíkot H1 és H2, hogy egy konvex halmaz S ponton y.

Tegyük fel, hogy két nem üres és B halmaz. GiperploskostH nazyvaetsyarazdelyayuschey hipersíkot, ha minden pont mnozhestvaA hazugság az egyik zárt félig terek által meghatározott giperploskostyuH. és az összes pontot mnozhestvaB rejlik egy másik meghatározott zárt felét. Sem tudja bizonyítani, több tételt az elválasztó hipersík. Tekintsük a legegyszerűbb őket. enged

- egy sor belső pontja mnozhestvaA.

3.1 Tétel. Puszta és b - két nem üres, konvex halmaz prichemØ. Aztán ott giperploskostH. elválasztó mnozhestvaA iB.1

Példák elválasztó hipersíkokat ábrán mutatjuk be. 3.3 és 3.4.

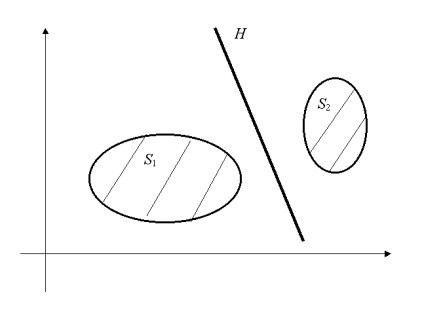
Ábra. 3.3. H hipersík elválasztja a készletek S1 és S2. nincs közös pontja

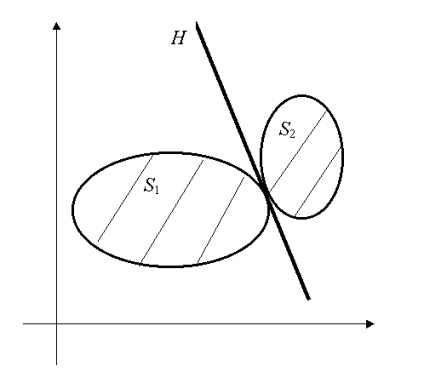
Ábra. 3.4. H hipersík elválasztja a készletek S1 és S2. egy közös pont

Konvex és konkáv függvények

Kapcsolódó cikkek

• Egy esszét a téma - az emberiség - iskola

• Konzultáció Konzultáció a témában a tanárok

• Előadás a kiválasztás