2- 3_Diskretnaya Matematika 3
Mi határozza meg a tulajdonságait a kapcsolat.
1) fényvisszaverő. mert . A visszaható grafikonok visszavert jelenlétében hurkot minden csúcs.
2) Ne tükröződésmentesítő. mert megléte reflexivitás - tagadta tükröződésmentes.
3) nem szimmetrikus. mert a pár jelenlétében végzett (1, 2) nincs párja (2, 1), és azt jelenti, sérül szabály (az oszlop nem szimmetrikus bordák).
4) Ne antiszimmetrikus. mert reflexív, akkor a szabályt megszegik prix = y.
6) tranzitivitás. mert ha «x osztó y» és «y elválasztó z», a «x osztó z». Oszlop az összes láncot kialakítani x-y - zárt él (x, y).
Például: (1, 3), (3, 6) (1, 6)
(1, 2), (2, 2) (1, 2), stb
7) Ne töltse. mert nem a bármely két X és Y lehet mondani, vagy. Például: (2, 5) R és (5, 2) R. Ezek csúcsokat élek kötik össze.
Így tehát az arány fényvisszaverő azonosan tranzitívan. eszközt egy megbízás kapcsán.
2) találni, hogy össze egy grafikon:
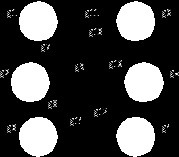
d) a sugár, átmérő, center, perifériás csúcsok;
Center egy csúcsa a grafikon, amely megvalósítja a legkisebb az eltérés. Centrumok lehetnek többszörös, hiszen eltérés csak a tip 1, ezért - Center.
Count sugara eltérést nevezzük a központtól p (G) = d (1) = 1.
Átmérő irányítatlan gráf közötti legnagyobb távolság csúcsot. És a távolság - a hossza a legkisebb elemi áramkör. Fgrafa átmérőjű is lehet nevezni
2) a maximális hossza egy elemi módon, majd a D (G) = 1.
A perifériás csúcs egy csúcs a legnagyobb eltérés. Ez egy 2, 3, 4, 5, 6.
e) A számos belső és külső stabilitás.
Belső stabil halmaza gráf G (x) - S egy részhalmaza csúcsok halmaza X. bármely két csúcsot, amelyek nem szomszédosak. A számos belső ellenállás α (G) - a maximális teljesítmény belsőleg stabil halmaza.
, ,
Külsőleg stabil halmaza gráf G (x) - T jelentése egy részhalmazában csúcsok minden csúcsa X., hogy a X \ T = arc csatlakozik a csúcsa a T.
A számú külső stabilitás β (G) - a minimális energiát külsőleg stabil halmaza. .
3) A két véletlenszerűen kiválasztott grafikonokat és megtalálják a Descartes-szorzat derékszögű összege.
a) több csúcsok X a Descartes-szorzat halmazok X1 és X2. azaz X1 × X2 =.
b) több csúcsot szomszédos vertex (x1, x2) egy Descartes-szorzat a két grafikon meghatározása a Descartes-szorzat készletek a gráf G1 (X1), a szomszédos X1 és a grafikon G2 (X2) szomszédos x2.
1) meghatározza a csúcsok halmaza G (X), és össze egy grafikon:
Peaks szomszédos egy.
A csúcsok szomszédos x. , TogdaG (a, x) =.